遗传算法(Genetic Algorithm, GA)是由美国Michigan大学的Hoiiand教授于1975年首先提出, 是一种借鉴生物界自然选择和自然遗传机制的随机化搜索算法[1]. 由于遗传算法通用性强, 被广泛应用于非线性、多目标、多变量、复杂的自适应系统中.
但是传统的遗传算法收敛速度慢、容易陷入局部最优, 尤其在计算复杂问题时无法求出最优解, 所以国内外学者对其进行了改进. 目前, 对遗传算法的改进主要体现在三个方面: 1) 对遗传算子进行动态调整, 最早由Srinvas等人提出[2,3]; 2) 对遗传算法的个体进行优化, 比如在文献[4]中提出个体可进化的适应度函数评价机制; 3) 采用1)和2)结合的方法改进遗传算法, 比如文献[5]提出的带基因修复的自适应遗传算法.
虽然近年来有大量的改进遗传算法被提出, 但是课题组在研究遗传算法时发现, 如果能够根据种群个体的分布情况动态调整遗传算子, 可以增强种群个体的多样性, 同时有利于加快算法收敛. 因此, 本文提出了一种带密度加权的自适应遗传算法—DWAGA (Adaptive Genetic Algorithm with Density Weighted), 该算法可以根据种群分布情况动态调整交叉和变异概率, 使得算法具有跳出局部极大值加快收敛速度的能力, 同时本文还对该算法的改进过程、方法进行了详细的分析, 最后通过求解三个函数的最优解验证了算法的有效性.
1 问题提出采用传统自适应遗传算法对如公式(1)所示函数进行最优求解, 并对其个体分布情况进行分析.
| $y = - {(x - 1)^2} + 4; x \in [ - 1,3]$ | (1) |
从图1可以看出, 遗传算法在第5代到第18代, 以及第25代–第95代之间停留了较长的时间, 虽然也进行交叉、变异等遗传操作, 但是由于种群过于集中于某一区域, 导致个体已近似相当, 即使进行了遗传操作, 但是变化不大. 尤其在算法迭代后期, 特别容易陷入局部最优解.
因此, 本文提出一种可以根据种群分布特点动态调整遗传算子的自适应遗传算法, 该算法旨在破坏种群的局部稳定性, 保持种群个体的多样性, 同时加快算法的收敛速度.

|
图 1 种群个体适应度分布图 |
2 改进的遗传算法——DWAGA 2.1 确定种群密度
种群初始化后, 对其个体按其适应度值由小到大的顺序进行排序, 如图2所示.

|
图 2 种群适应度值分布图 |
图2中, M表示种群规模, fmax表示当代种群中个体的最大适应度值, fmin表示当代种群中个体的最大适应度值, favg表示当代种群个体的平均适应度值. 为了便于进行下一步的描述, 做如下定义.
群体范围:
| $H = {f_{\max }} - {f_{\min }}$ |
某个体到适应度平均值处的距离(f表示要变异个体的适应度值):
| $h = \left| {f - {f_{avg}}} \right|$ |
中心区域半径:
| $\delta = \frac{H}{{M - 1}}$ |
到适应度平均值处距离小于δ的种群个数:
| $N(\delta ,{f_{avg}})$ |
种群中心区域密度:
| $\rho = \frac{{N(\delta ,{f_{avg}})}}{M}$ |
从模式理论[1]可知, 当选择策略确定后影响遗传算法收敛性的主要因素是由遗传算子来决定的. Srinvas首先提出了自适应遗传算法[2], 其思想是当种群个体适应度值低于种群平均适应度值时, 说明个体性能较差, 增大交叉概率Pc和变异概率Pm, 使得该个体被破坏或者淘汰; 相反, 当种群个体适应度值高于种群平均适应度值时, 说明种群个体优良, 相应地减小Pc和Pm, 使该个体得以保存到下一代中. 其中计算交叉概率和变异概率的公式如下:
| ${P_c} = \left\{ {\begin{array}{*{20}{l}}{{P_c}\displaystyle\frac{{({f_{\max }} - {f'})}}{{{f_{\max }} - {f_{avg}}}},({f'} \ge {f_{avg}})}\\{{P_c},({f'} < {f_{avg}})}\end{array}} \right.$ | (2) |
| ${P_m} = \left\{ {\begin{array}{*{20}{l}}{{P_m}\displaystyle\frac{{({f_{\max }} - {f'})}}{{{f_{\max }} - {f_{avg}}}},({f'} \ge {f_{avg}})}\\{{P_m},({f'} < {f_{avg}})}\end{array}} \right.$ | (3) |
式中, fmax表示当代种群中个体的最大适应度值, fmin表示当代种群中个体的最大适应度值, favg表示当代种群个体的平均适应度值, f’表示要变异个体的适应度值.
从公式(2)和公式(3)中看出, 当种群适应度值等于最大适应度值时, 交叉概率和变异概率的值为零, 这样就过分地保留了种群在前期进化阶段适应度值最大的个体, 使得种群进化过程缓慢, 极易陷入局部最优解. 基于这个原因, 段玉倩等人对上述自适应遗传算法进行了改进[3].
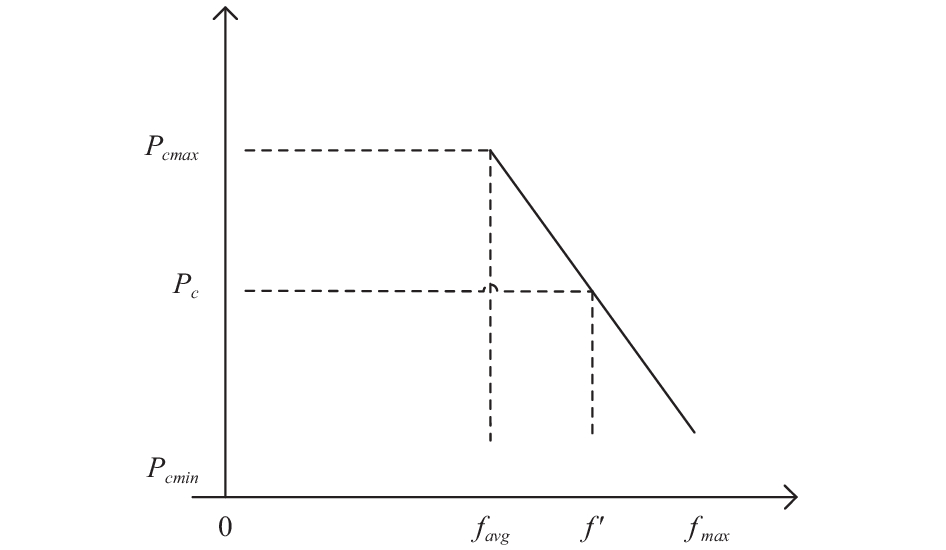
如图3所示, 在改进的自适应遗传算法中, 设置种群交叉概率的最大值和最小值, 且最小值不等于零. 在种群个体为最大适应度值时, 仍可以以最小的交叉概率来进行操作, 这样就使得种群个体不会处于一种停滞不变的状态. 计算交叉概率的公式如下式(4), 变异概率计算公式类似, 省略.
| ${P_c} = \left\{ {\begin{array}{*{20}{l}}{{P_{c\max }} - ({P_{c\max }} - {P_{c\min }})\displaystyle\frac{{({f_{\max }} - {f'})}}{{{f_{\max }} - {f_{avg}}}},({f'} \ge {f_{avg}})}\\{{P_{c\max }},({f'} < {f_{avg}})}\end{array}} \right.$ | (4) |
|
图 3 自适应遗传算法交叉概率取值图 |
公式(3)虽然改善了公式(1)和(2)中存在的不足, 但仍缺乏对种群整体分布的分析, 尤其是若种群个体过分集中于某一区域, 则容易陷入局部最优解. 因此, 本文在上述自适应遗传算法的基础上[3-5], 提出带密度加权的自适应遗传算法. 依据种群中心区域密度ρ对Pc作出修正, 如公式(5).
| ${P_c} = \left\{ {\begin{array}{*{20}{l}}{{P_{c\max }} \cdot A\rho ,(h \le \delta )}\\{{P_{c\max }} - \displaystyle\frac{{({P_{c\max }} - {P_{c\min }})({f_{\max }} - {f'})}}{{{f_{\max }} - {f_{avg}} + \alpha }} \cdot A\rho ,(h > \delta ,{f'} < {f_{avg}})}\\{{P_{c\max }} - \displaystyle\frac{{({P_{c\max }} - {P_{c\min }})({f_{\max }} - {f'})}}{{{f_{\max }} - {f_{avg}} + \alpha }} \cdot A(1 - \rho ),(h > \delta ,{f'} \ge {f_{avg}})}\end{array}} \right.$ | (5) |
式(4)中A为常数, 其值大小反映了对种群中心区域密度的重视程度. α为极小的常数, 防止分母为零导致的错误, 通常取值为极小的数. 0<Pcmin<Pcmax<1, 本文中Pcmax=0.9, Pcmin=0.4. ρ为种群中心区域密度. 其他符号的意义同前不变.
当h小于等于δ时, 种群个体适应度分布不均匀, 在个体适应度平均值处(中心区域)集中, 容易陷入局部最优解. 因此, 采用增大中心区域个体的交叉概率, 破坏该区域个体的稳定性, 使得该个体被淘汰或者在交叉过程中产生新的个体, 以此实现跳出局部极值的能力.
当h大于δ时, 种群个体适应度分布均匀, 对于适应度低于平均适应度的个体, 取较高的Pc, 使该个体被淘汰掉; 而高于群体平均适应度的个体, 取较低的Pc使个体得以保护进入下一代.
同理可以得到自适应遗传算法变异概率的计算公式, 如公式(6).
| ${P_m} = \left\{ \begin{array}{l}{P_{m\max }} \cdot A\rho ,(h \le \delta )\\{P_{m\max }} - \displaystyle\frac{{({P_{m\max }} - {P_{m\min }})({f_{\max }} - f)}}{{{f_{\max }} - {f_{avg}} + \alpha }} \cdot A\rho ,(h > \delta ,f < {f_{avg}})\\{P_{m\max }} - \displaystyle\frac{{({P_{m\max }} - {P_{m\min }})({f_{\max }} - f)}}{{{f_{\max }} - {f_{avg}} + \alpha }} \cdot A(1 - \rho ),(h > \delta ,f \ge {f_{avg}})\end{array} \right.$ | (6) |
式中, 0<Pmmin<Pmmax<1, 本文中Pmmax=0.1, Pmmin=0.01. 其他符号的意义同前不变.
3 DWAGA算法性能分析 3.1 评估函数[6,7] 3.1.1 一元函数函数表达式为:
| $\begin{array}{c}{F_1}(x) = x\sin (10\pi x) + 2.0,\\x \in [ - 1,2]\end{array}$ | (7) |
该函数为一元多峰值函数, 其函数值随自变量变化如图4所示. 在其定义域内有全局最大值3.85, 在整个定义域内, 该函数还存在多个极大值, 呈台阶式分布. 该一元函数用来考查算法在存在多个极值时的搜寻能力.

|
图 4 一元函数图像 |
3.1.2 Schaffer函数
函数表达式为:
| $\begin{aligned}{F_2}({x_1},{x_2}) =& 0.5 - \displaystyle\frac{{{{\sin }^2}\sqrt {x_1^2 + x_2^2} - 0.5}}{{{{[1 + 0.001(x_1^2 + x_2^2)]}^2}}}&{x_1},{x_2} \in [ - 10,10]\end{aligned}$ | (8) |
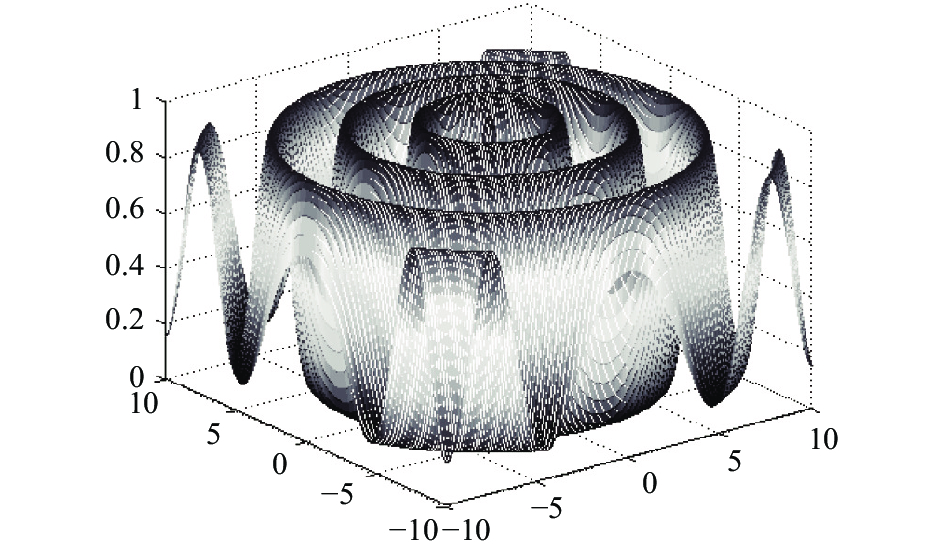
该函数在其定义域内有最大值F2(0, 0)=1, 但是在极大点附近有由全局次优点F2(x1, x2)=0.99形成的圈脊, 如果算法局部搜索能力较弱, 则极易收敛于次优点. 其函数值随自变量变化如图5所示. 此函数将用以考查算法在全局最优点被局部最优解包围时从局部最优跳离的能力.
|
图 5 Schaffer函数图像 |
3.1.3 De Jone’s函数
函数表达式为:
| $\begin{array}{c}{F_3}({x_1},{x_2}) = 0.002 + \sum\limits_{j = 1}^{25} {\displaystyle\frac{1}{{j + \sum\limits_{i = 1}^2 {{{({x_i} - {a_{ij}})}^6}} }}}, \;\;{x_i} \in [ - 40,40],\\{a_{ij}} = {\left[ {\begin{array}{*{20}{c}}{ - 32, - 16,0,16,32,..., - 32, - 16,0,16,32}\\{ - 32, - 32, - 32, - 32, - 32,...,32,32,32,32,32}\end{array}} \right]_{2 \times 25}}\end{array}$ | (9) |
|
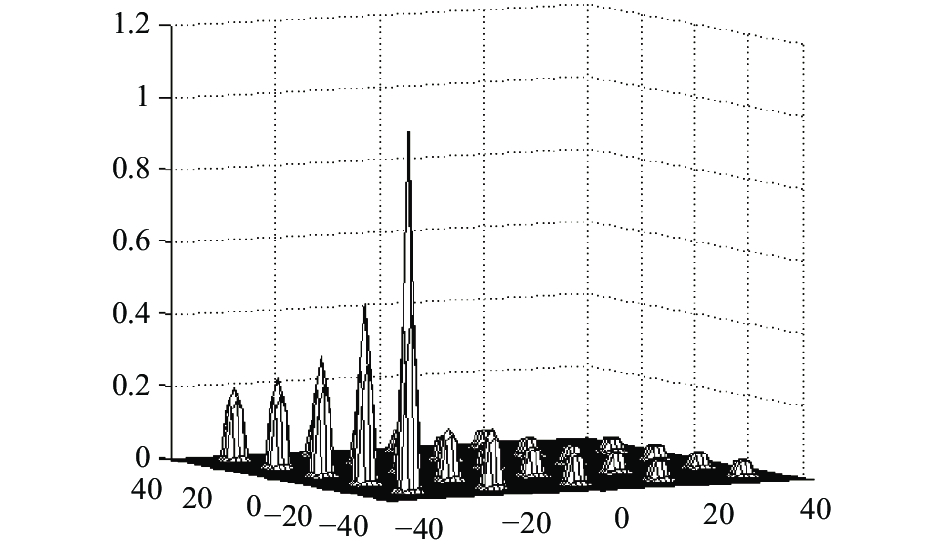
图 6 De Jone’s函数图像 |
该函数为二维区域的多峰值函数, 在其定义域内共有25个局部极大值, 呈跳跃状分布在独立的区域内, 极大值点自变量之间变化幅值大, 极易使算法陷入局部最大值点而停止进化, 其函数值随自变量变化如下图6所示. 其中, 该函数的全局最大值点为F3(–32, –32)=1. 该函数用来考查算法在存在多个极值的二维函数中的寻优能力.
3.2 实验结果与分析为了验证算法的有效性, 文中采用表1中的测试条件, 对上述3个函数进行500次寻优计算, 在收敛次数、平均收敛代数、以及最佳适应度值三方面对自适应遗传算法(Adaptive Genetic Algorithm, AGA)、改进的自适应遗传算法(Improve Adaptive Genetic Algorithm, IAGA), 以及本文提出的带密度加权的自适应遗传算法(Adaptive Genetic Algorithm with Density Weighted, DWAGA)进行了统计和比较, 详见表2, 表3, 表4.
| 表 1 测试条件 |
| 表 2 F1收敛性能 |
| 表 3 F2收敛性能 |
| 表 4 F3收敛性能 |
从表2、表3、表4的实验结果可以看出, 在3个测试函数下, 文中提出的DWAGA算法收敛总次数最多. 同时, 改进的自适应遗传算法收敛代数明显快于标准的自适应遗传算法, 其中本文提出的DWAGA收敛速度最快.
同时, 为了分析AGA、IAGA、DWAGA这3种算法在整个迭代周期上的性能, 文中分别列出了在不同测试函数下3种算法的适应度平均值分布图, 如图7所示.
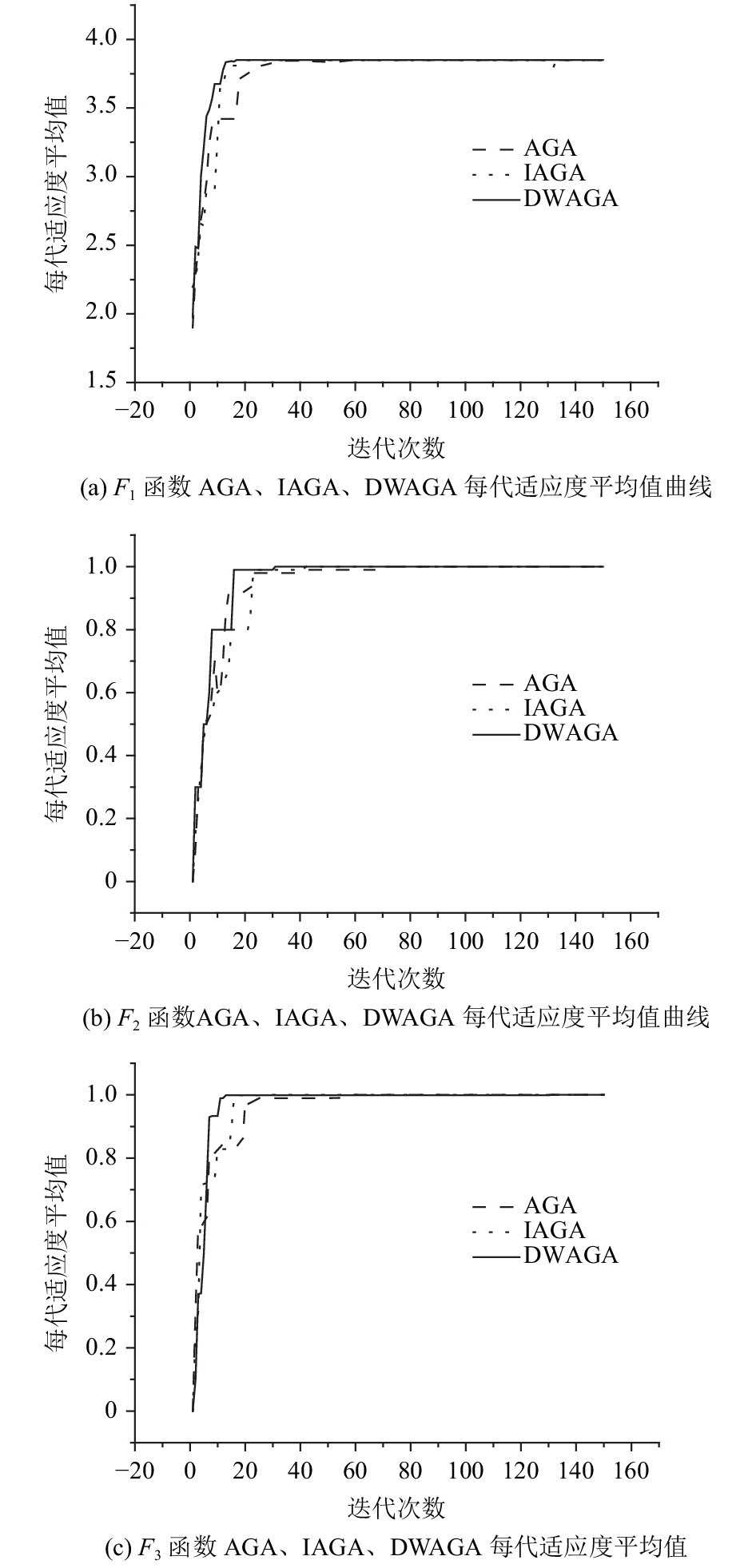
|
图 7 AGA、IAGA、DWAGA算法在三种测试函数下每代适应度平均值曲线图 |
从图7中可以看出, AGA算法在迭代中期长期保持不变, IAGA和DWAGA算法都得到了改善, 其中DWAGA算法改善最为明显, 收敛速度最快. 同时, 文中三个测试函数的适应度函数就是函数的表达式, 因此都是求解相应函数的全局最大值点, 通过图7的比较, AGA和IAGA算法都多次停留在局部极值处, 但是本文提出的DWAGA算法能够快速跳出局部极值, 向最大值点处收敛, 有效地提高了算法的收敛速度.
4 结论通过对传统的自适应遗传算法进行了深入研究, 针对其收敛速度慢、难以跳出局部极大值的情况, 本文提出DWAGA算法进行改善, 通过对三个函数求解最优解的实验, 表明该算法在收敛速度、平均收敛次数, 以及全局最大值的搜寻能力上都明显优于传统自适应遗传算法, 从而验证该算法的有效性和鲁棒性.
| [1] |
Holland JH. Adaptation in natural and artificial system: An introductory analysis with applications to biology, control and artificial intelligence. Cambridge, MA: MIT Press, 1992.
|
| [2] |
Srinivas M, Patnaik LM. Adaptive probabilities of crossover and mutation in genetic algorithms. IEEE Transactions on Systems, Man, and Cybernetics, 1994, 24(4): 656-667. DOI:10.1109/21.286385 |
| [3] |
段玉倩, 贺家李. 遗传算法及其改进. 电力系统及其自动化学报, 1998, 10(1): 39-52. |
| [4] |
林明玉, 黎明, 周琳霞. 基于可进化性的自适应遗传算法. 计算机工程, 2010, 36(20): 173-175. DOI:10.3969/j.issn.1000-3428.2010.20.061 |
| [5] |
刘冀成, 胡雅毅. 带基因修复策略的自适应遗传算法. 计算机应用, 2006, 26(6): 1401-1402, 1405. |
| [6] |
Wang SH, Lu ZY, Wei L, et al. Fitness-scaling adaptive genetic algorithm with local search for solving the multiple depot vehicle routing problem. Simulation, 2016, 92(7): 601-616. DOI:10.1177/0037549715603481 |
| [7] |
Deng Y, Liu Y, Zhou DY. An improved genetic algorithm with initial population strategy for symmetric TSP. Mathe-matical Problems in Engineering, 2015, 2015: 212749. |
| [8] |
曲志坚, 张先伟, 曹雁锋, 等. 基于自适应机制的遗传算法研究. 计算机应用研究, 2015, 32(11): 3222-3225, 3229. DOI:10.3969/j.issn.1001-3695.2015.11.004 |
 2018, Vol. 27
2018, Vol. 27

