河道洪水演算是根据河道上游水情推求下游水情的一种洪水预报方法, 在防洪规划和水库调洪计算中有着重要的作用. 马斯京根模型是自然河道和河流中最常用的洪水演算方法之一, 它是美国著名科学家McCarthy GT在1938年研究了马斯京根河流域后首次提出的[1]. 采用马斯京根模型进行洪水演算时, 由于参数值不能从历史入流和出流水文图得到, 所以模型的参数估计问题成为最重要的任务. 求解马斯京根模型参数的传统方法有试错法[2]、最小二乘法[3]和非线性规划法[4]等, 这些方法在实际应用中计算过程复杂, 不具有足够的稳定性和高效性. 因此, 近年来许多学者将智能优化算法应用于马斯京根模型参数估计, 并取得了较好的优化效果, 如遗传算法[5]、差分进化算法(DE)[6]、入侵杂草优化算法[7]、飞蛾火焰算法[8]和免疫克隆选择算法[9]等. 然而, 由于马斯京根模型本身的近似性及这些算法存在早熟收敛和易陷入局部极值等问题, 使得洪水演算的精度并不十分理想.
受自然界中灰狼的社会等级制度和捕食行为的启发, 学者Mirjalili S等人[10]在2014年提出了一种新型元启发式算法, 称为灰狼优化算法 (Grey Wolf Optimizer, GWO). 算法的优点主要是结构简单、需要设置的参数少和在实验编码中容易实现等, 且研究结果表明其优化性能优于DE算法、PSO算法和引力搜索算法. 然而, 基本GWO算法存在依赖初始种群、易陷入局部最优和难以协调其探索和开发能力等缺点, 针对这些缺点, 本文对基本GWO算法进行了改进, 利用混沌Chebyshev映射产生初始灰狼种群, 增强全局搜索过程中的种群多样性; 给出一种随机分布调整收敛因子策略, 以平衡算法的全局搜索和局部搜索能力. 采用7个基准测试函数对比仿真验证了改进GWO算法(IGWO)的有效性. 最后用IGWO算法来估计马斯京根模型中的参数, 对1961年称沟湾至临清段洪水进行演算, 与现有的其它参数估计方法进行了对比分析.
1 马斯京根模型理论马斯京根模型是一种常用的河道洪水演算方法,该方法利用河段水量槽蓄方程代替复杂的水动力方程, 极大地简化了计算. 其基本方程为[9]:
| $\left\{ {\begin{aligned} & {\displaystyle\frac{{{\rm{d}}W}}{{{\rm{d}}t}} = I - Q} \\ & {W = K\left[ {xI + \left( {1 - x} \right)Q} \right]} \end{aligned}} \right.$ | (1) |
式(1)中, W为河段的槽蓄量, t为时间, I和Q分别为河段的入流量和出流量, x为流量比重因子, K为槽蓄系数.
式(1)的差分解为
| $\left\{ {\begin{array}{*{20}{l}} {\tilde Q\left( 1 \right) = Q\left( 1 \right)} \\ {\tilde Q\left( i \right) = {C_0}I\left( i \right) + {C_1}I\left( {i - 1} \right) + {C_2}\tilde Q\left( {i - 1} \right),i = 2,3,\cdots,n} \end{array}} \right.$ | (2) |
式(2)中,
| ${C_0} + {C_1} + {C_2} = 1$ | (3) |
根据式(2)、(3)建立马斯京根模型的参数优化模型, 优化模型如下:
| $\begin{split}& \min F = {\displaystyle\sum\limits_{i = 2}^n {\left( {\left| {{C_0}I\left( i \right) + {C_1}I\left( {i - 1} \right) + {C_2}\tilde Q\left( {i - 1} \right) - Q\left( i \right)} \right|} \right)} ^q}\\& {\rm{s}}.{\rm{t}}.\;\;\;\;\;\;{g_1}:{C_0} \in \left[ {0,1} \right]\\& \;\;\;\;\;\;\;\;\;\;\;{g_2}:{C_1} \in \left[ {0,1} \right]\\& \;\;\;\;\;\;\;\;\;\;\;{g_3}:1 - {C_0} - {C_1} \in \left[ {0,1} \right]\end{split}$ | (4) |
文中取常数
| $\min f = F + p\left( {{g_3}\left( {{C_0},{C_1}} \right)} \right)$ | (5) |
式(5)中
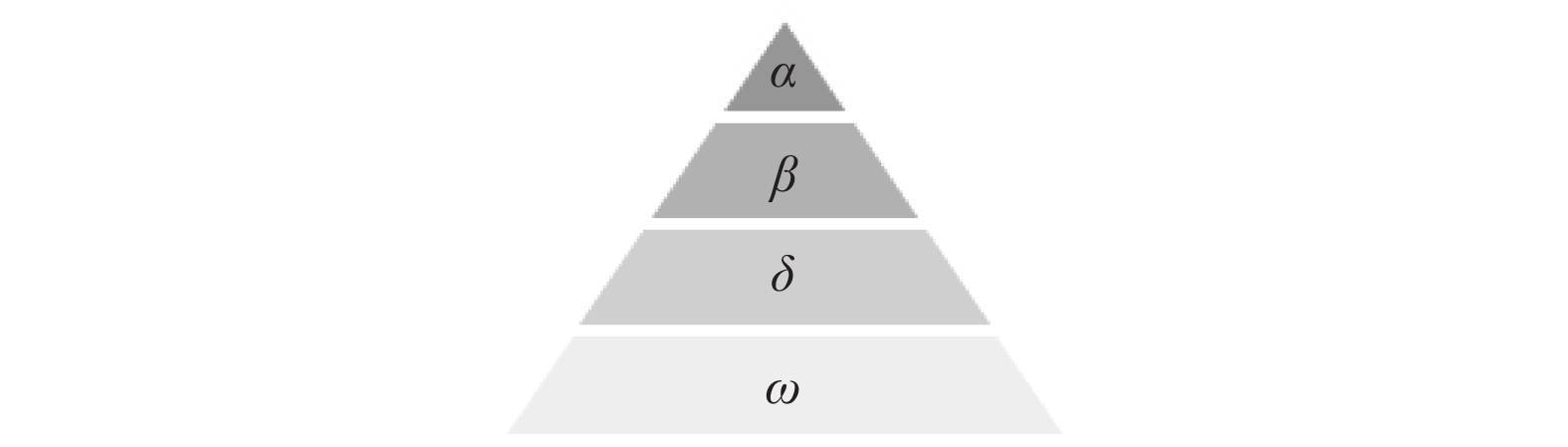
GWO算法[10]是通过模拟自然界中灰狼群体的社会等级机制和捕食行为而提出的一种新型群体智能优化算法. 灰狼种群具有严格的等级制度, 如图1所示.
|
图 1 灰狼等级示意图 |
图1中, α是最高级别的灰狼, β是α的下属灰狼, δ服从α及β的命令, 等级最低的灰狼称为ω. 灰狼群体严格的社会等级机制在实现群体高效捕杀猎物的过程中发挥着至关重要的作用. 在捕食猎物时, 群体中其它灰狼在头狼α 的带领下有组织地对猎物进行围攻. 首先, 狼群通过气味等信息追踪、靠近猎物; 然后, 狼群包围猎物, 直到猎物停止移动; 最后, 攻击猎物.
假设灰狼种群数目为N, 灰狼的位置为X. 群体最优解为α, 次优解为β, 第三最优解为δ, 其它个体为ω. 则灰狼捕食行为的数学模型描述如下:
| ${{D}} = \left| {{{C}} \cdot {{{X}}_p}\left( t \right) - {{X}}\left( t \right)} \right|$ | (6) |
| ${{X}}\left( {t + 1} \right) = {{{X}}_p}\left( t \right) - {{A}} \cdot {{D}}$ | (7) |
其中, t表示当前迭代次数, A和C是系数向量,
| ${{A}} = 2a \cdot {{{r}}_1} - a$ | (8) |
| ${{C}} = 2 \cdot {{{r}}_2}$ | (9) |
其中,
种群中其它灰狼的位置由α、β和δ的位置共同决定:
| $\left\{ {\begin{array}{*{20}{c}}{{{{D}}_\alpha } = \left| {{{{C}}_1} \cdot {{{X}}_\alpha } - {{X}}} \right|,\;\;\;{{{X}}_1} = {{{X}}_\alpha } - {{{A}}_1} \cdot {{{D}}_\alpha }}\\{{{{D}}_\beta } = \left| {{{{C}}_2} \cdot {{{X}}_\beta } - {{X}}} \right|,\;\;\;{{{X}}_2} = {{{X}}_\beta } - {{{A}}_2} \cdot {{{D}}_\beta }}\\{{{{D}}_\delta } = \left| {{{{C}}_3} \cdot {{{X}}_\delta } - {{X}}} \right|,\;\;\;\;{{{X}}_3} = {{{X}}_\delta } - {{{A}}_3} \cdot {{{D}}_\delta }}\end{array}} \right.$ | (10) |
| ${{X}}\left( {t + 1} \right) = \frac{{{{{X}}_1} + {{{X}}_2} + {{{X}}_3}}}{3}$ | (11) |
GWO算法自提出以来已在许多领域得到了应用, 但其仍存在依赖初始种群和易陷入局部最优的缺点. 为了解决这些问题, 对基本GWO算法作如下改进:
(1) 混沌种群初始化
基本GWO算法在搜索空间中随机初始化灰狼种群, 容易造成灰狼位置分布不均匀, 导致种群多样性差. 混沌映射具有较好的遍历性和不重复性, 因此可以用来代替种群随机初始化. 本文采用Chebyshev混沌映射产生灰狼种群的初始位置, 映射方程[11]为:
| ${x_{n + 1}} = \cos \left( {k{\rm{cos}^{ - 1}}\left( {{x_n}} \right)} \right)$ | (12) |
式(12)中k为阶次, 当
(2) 随机分布调整收敛因子
由文献[10]可知, 当|A|>1时, 灰狼群体将扩大搜索范围寻找猎物, 即全局搜索; 当|A|<1时, 灰狼群体将收缩搜索范围对猎物进行攻击, 即局部搜索. 因此,A的大小与GWO算法的全局搜索和局部搜索能力有很大关系. 由公式(8)可以看出, A随着收敛因子
若将收敛因子a设定为服从某种分布的随机数, 利用随机变量的特性调整控制参数, 既能在进化初期有机会取得较大或较小的值, 又能在进化后期取得较小或较大的值, 从而协调GWO算法的探索和开发能力. 基于上述分析, 受文献[12]的启发, 本文提出一种随机分布调整收敛因子策略:
| $a = \left( {{a_{\max }} - {a_{\min }}} \right)rand() + \sigma randn()$ | (13) |
式(13)中, amax、amin是收敛因子的最大值和最小值, rand()是[0, 1]均匀分布的随机数, randn()是正态分布的随机数, σ是标准差.
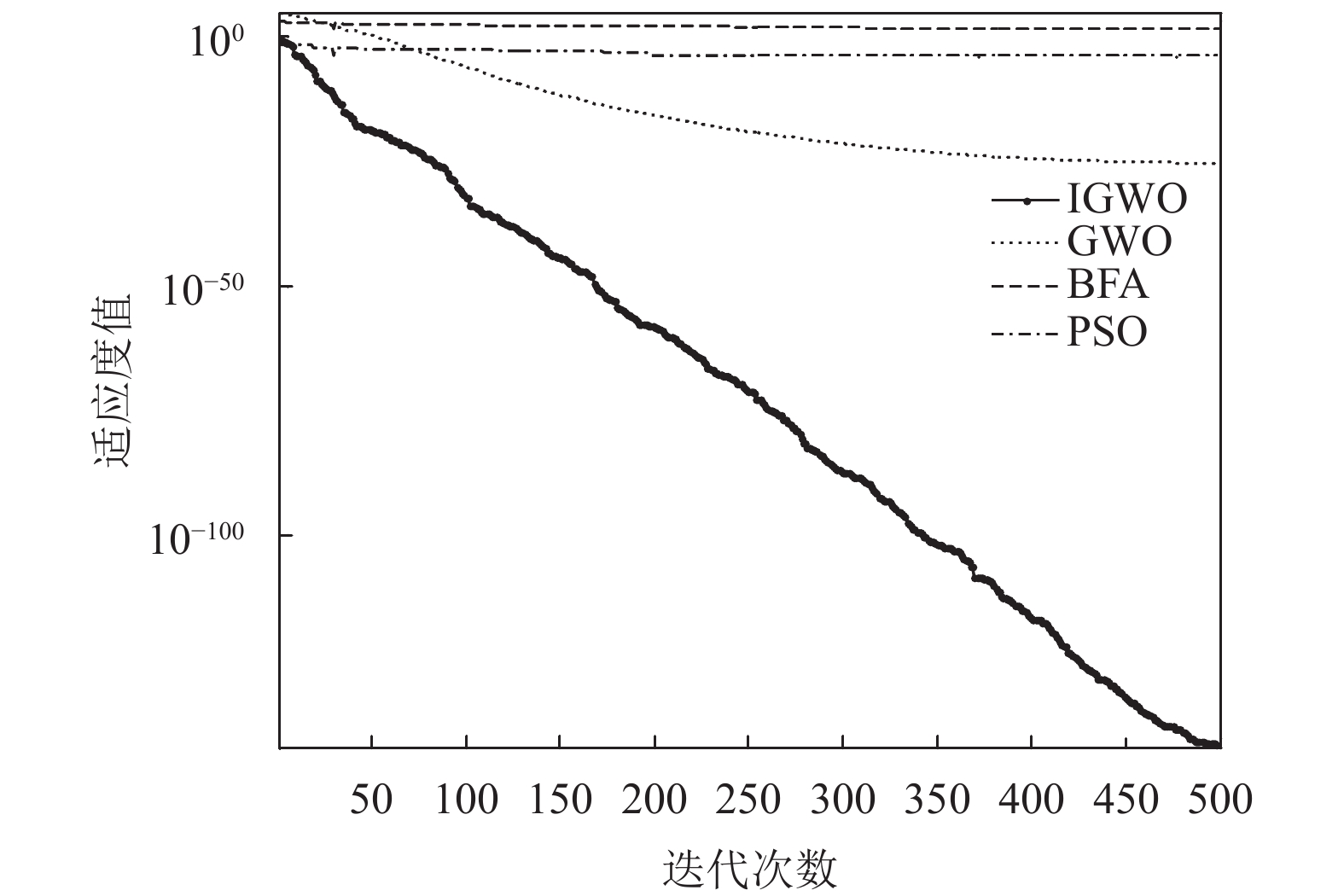
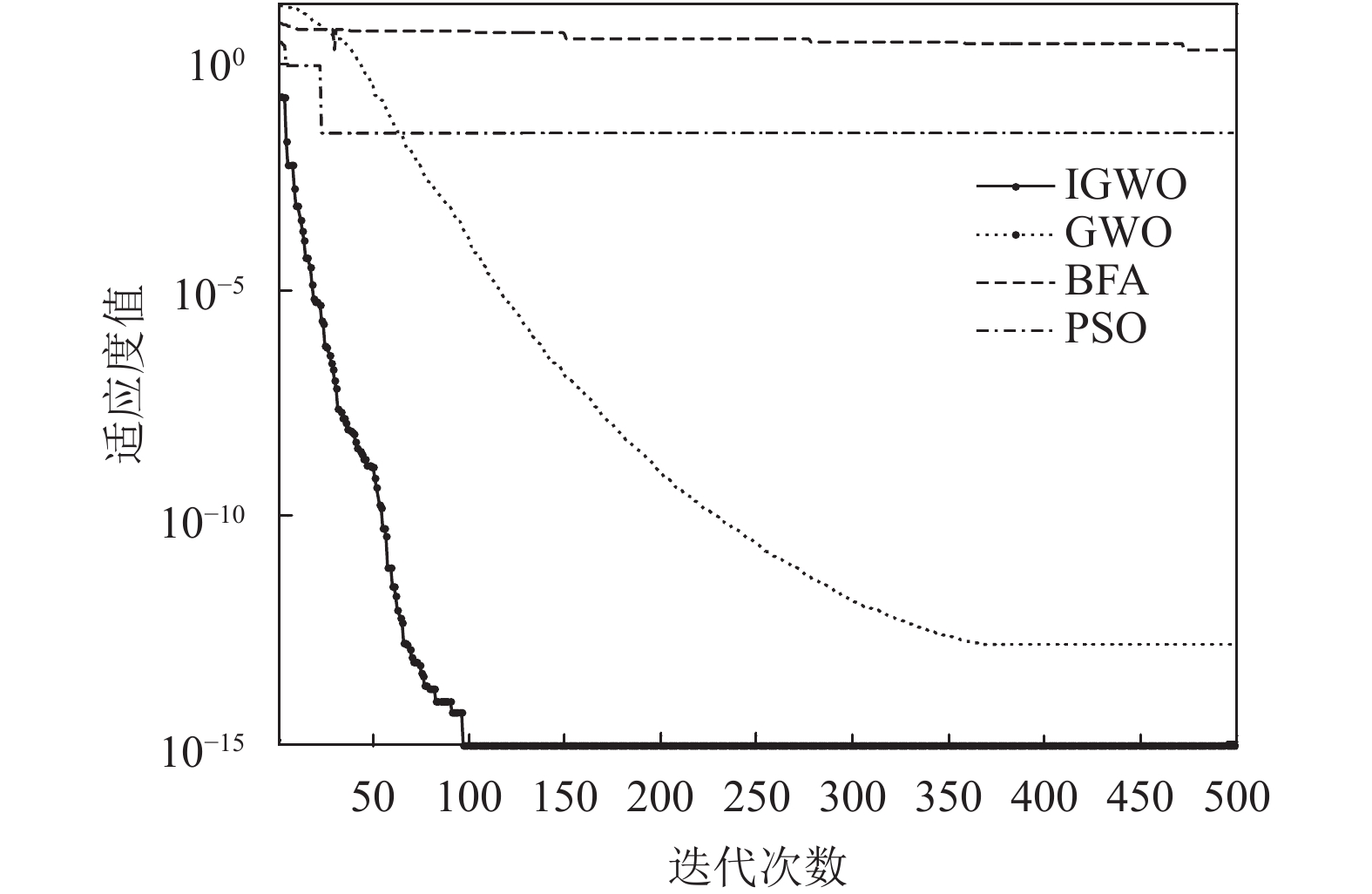
2.3 仿真实验为了验证IGWO算法的性能, 利用其对国际上通用的7个经典测试函数进行求解, 并与基本GWO算法、PSO算法和细菌觅食算法(BFA)进行对比, 比较结果如表1所示. 其中PSO算法是通过模拟自然界鸟群觅食行为来寻找最优解的一种演化算法. BFA算法是基于大肠杆菌觅食行为提出的一种仿生类群体智能算法. 同时给出了Sphere函数和Ackley函数的收敛曲线图, 如图2和图3所示.
算法的参数设置: 各算法的种群规模均为30, 最大迭代次数为500, PSO算法中粒子速度Vmax=5, c1=c2=0.5; BFA算法中最大趋化代数Nc=20, 最大前进步数Ns=4, 复制操作执行次数Nre=10, 迁徙操作执行次数Ned=2, 迁徙概率Ped=0.25.
| 表 1 4种进化算法结果比较 |
从表1的数据结果可以看出, 在种群规模和最大迭代次数设置相同的情况下, 与基本GWO算法、PSO算法和BFA算法相比, IGWO算法在7个测试函数上均表现出了较好的寻优性能, 收敛精度有较大的提高, 特别是Rastrigin 函数收敛到了理论最优值. 从图2和图3可以看出, IGWO算法具有更高的求解精度和更快的收敛速度.
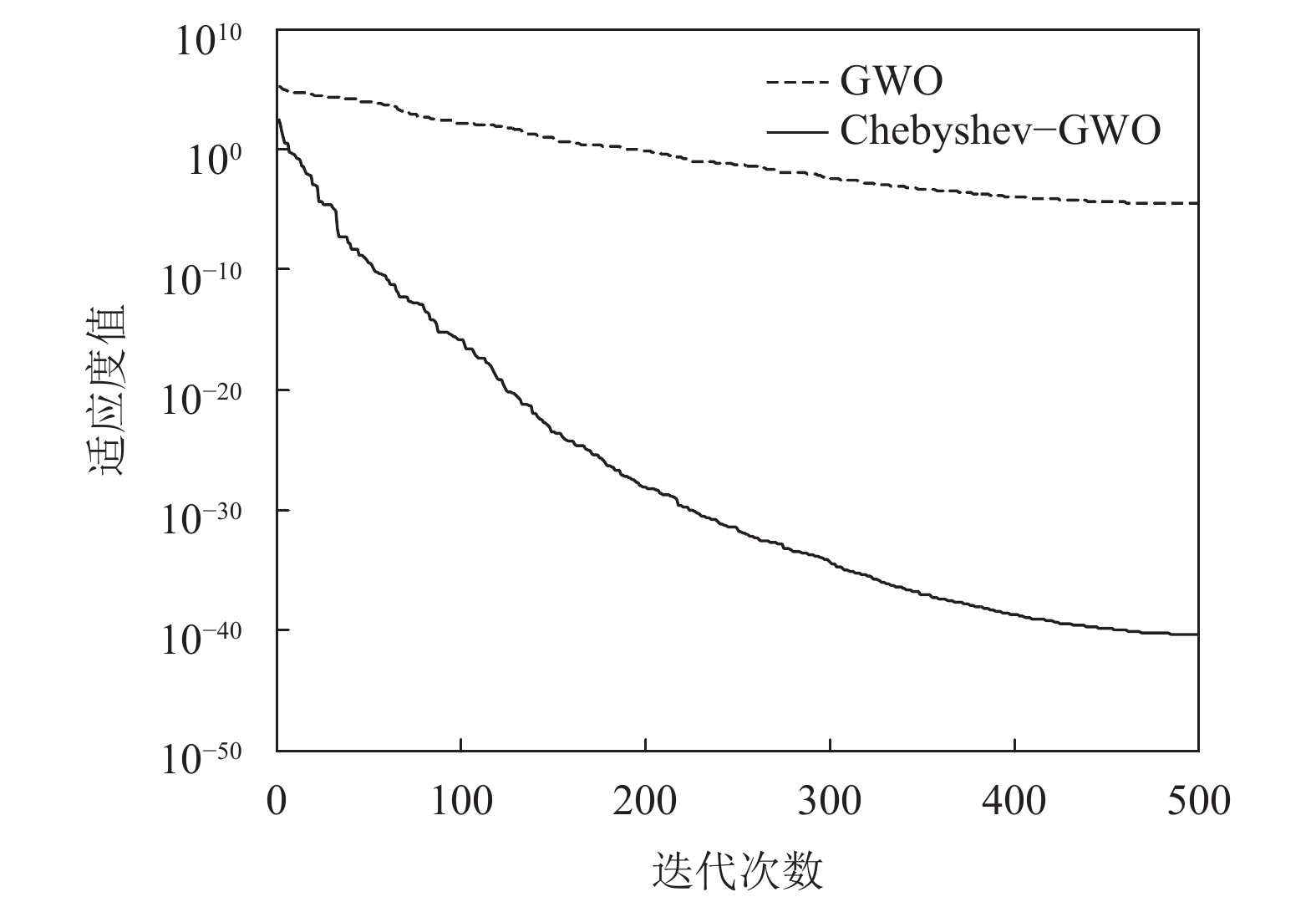
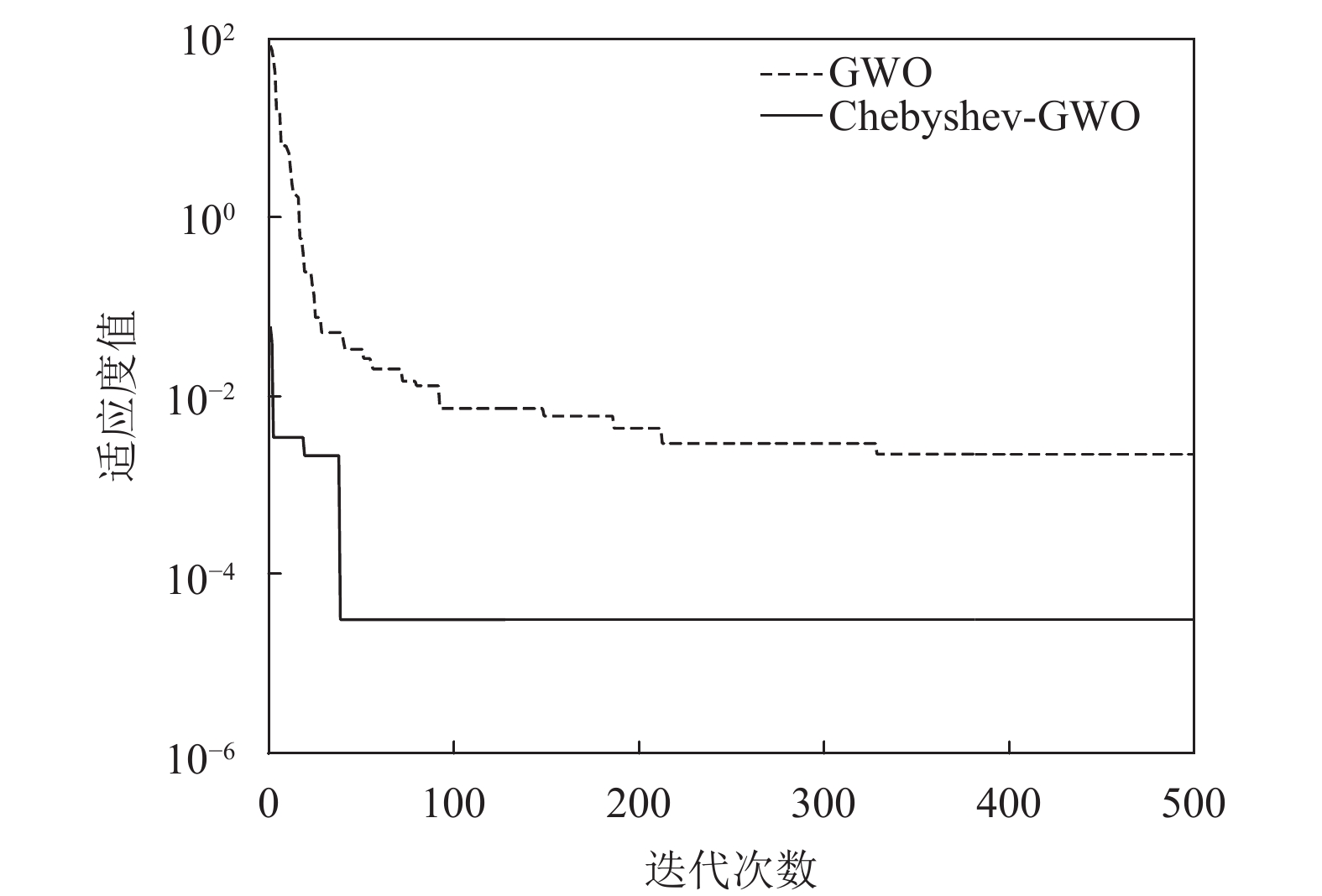
下面验证Chebyshev混沌初始化策略对算法性能的影响. 图4和图5给出了Schwefel 1.2函数和Quartic函数在不同初始化策略下的收敛曲线, GWO表示随机初始化种群, Chebyshev-GWO表示Chebyshev混沌初始化. 从图4和图5可以看出, 本文所采用的Chebyshev映射初始化种群策略, 有效地提高了算法的收敛精度和收敛速度.
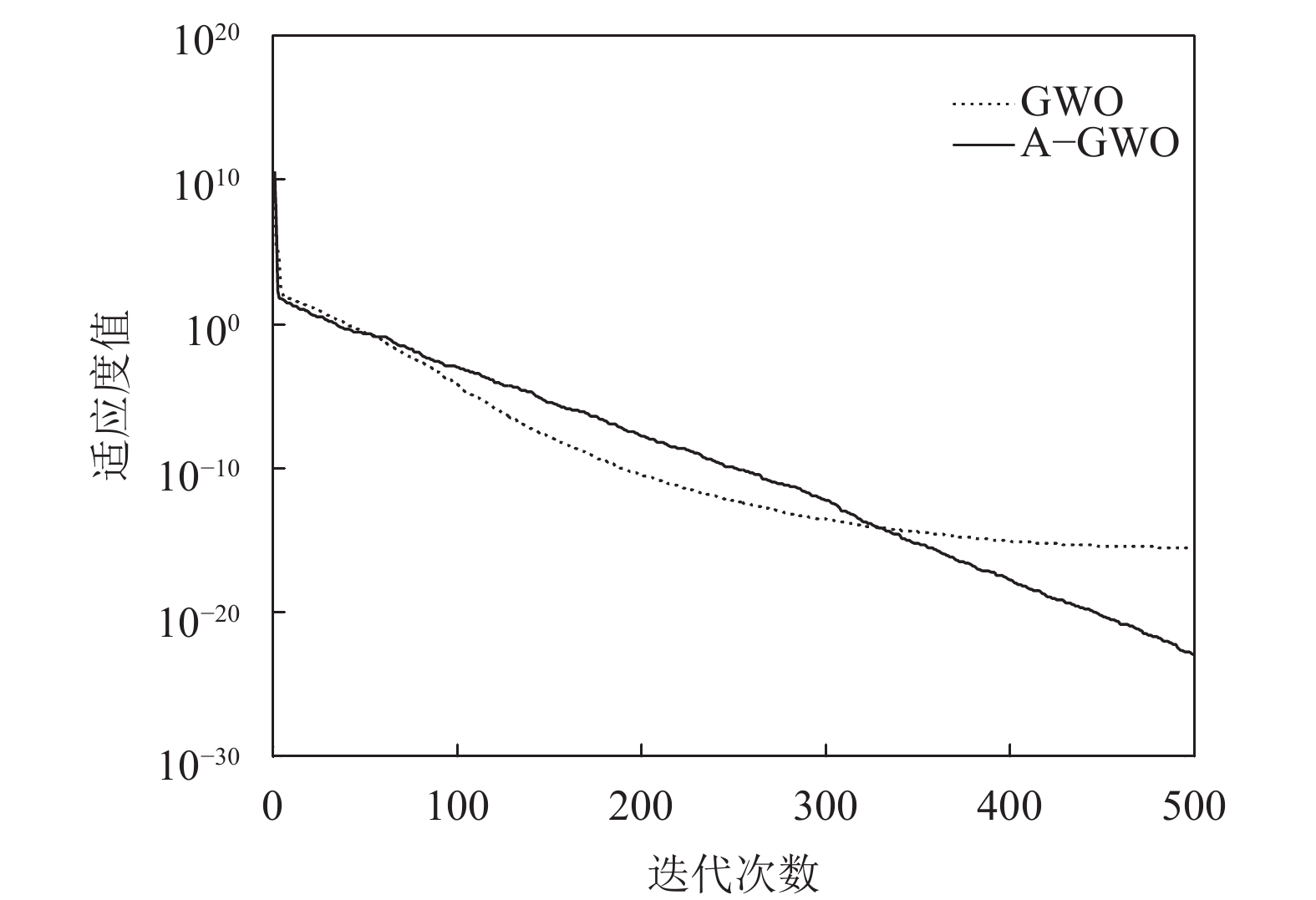
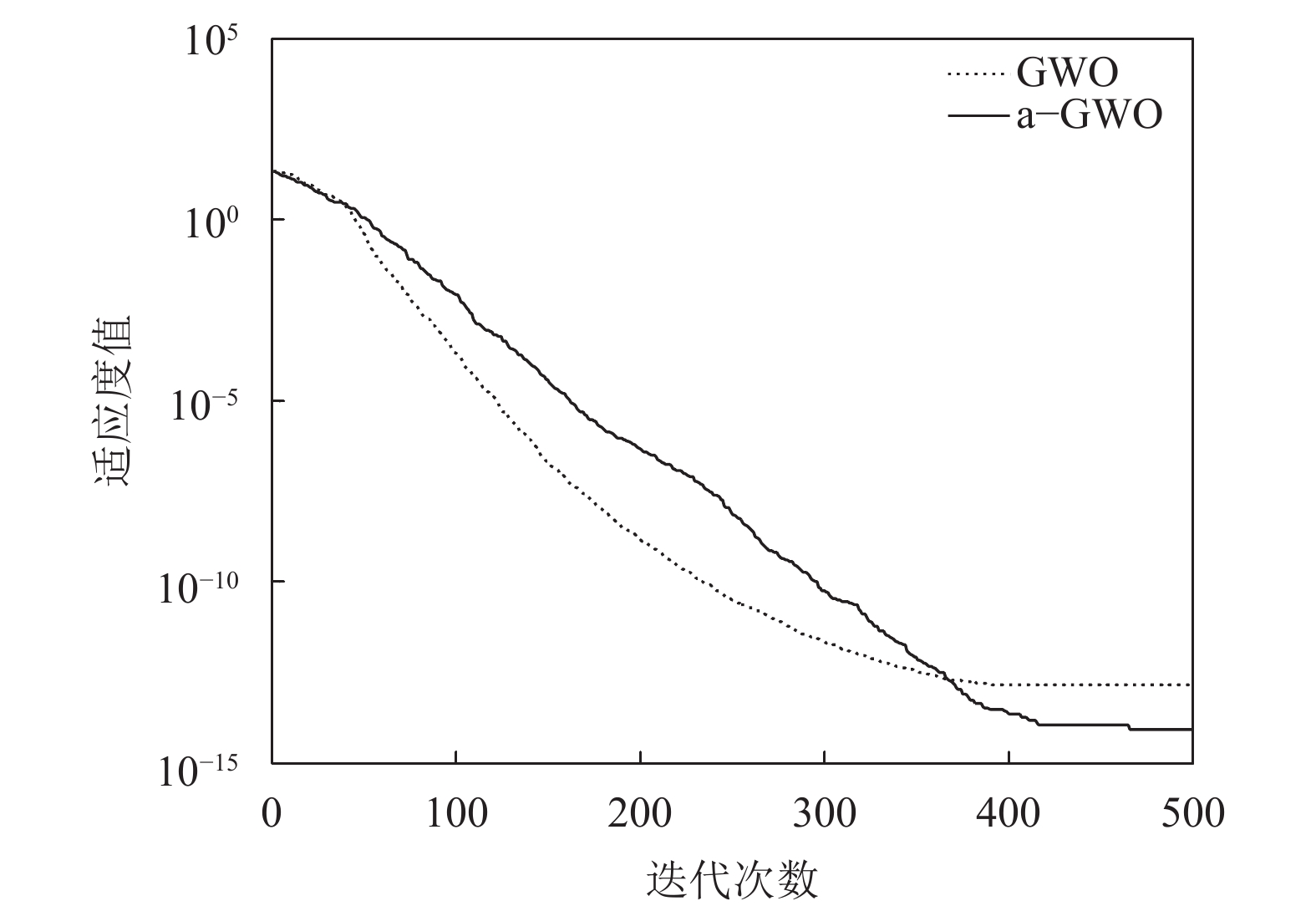
此外, 讨论文中给出的随机调整收敛因子策略对算法性能的影响. 图6和图7是Schwefel 2.22函数和Ackley函数采用不同收敛因子时的收敛曲线, GWO表示收敛因子线性递减的GWO算法, a-GWO表示随机调整收敛因子的GWO算法. 从图6和图7可以看出, 本文提出的随机调整收敛因子策略能有效地提高算法的收敛精度.
|
图 2 Sphere函数收敛曲线 |
|
图 3 Ackley函数收敛曲线 |
|
图 4 Schwefel 1.2函数在不同初始化策略下的收敛曲线 |
3 马斯京根模型的参数估计步骤
利用改进的灰狼优化算法(IGWO)估计马斯京根模型参数时, 每头灰狼的位置对应一组解, 以实际流量和演算流量的最小绝对误差和为目标函数, 运用IGWO对目标函数进行求解, 即以式(5)作为目标函数, 寻找f的最小值, 对应于最优准则函数值. 灰狼的个体位置为一个2维矢量
|
图 5 Quartic函数在不同初始化策略下的收敛曲线 |
|
图 6 Schwefel 2.22函数在不同收敛因子下的收敛曲线 |
|
图 7 Ackley函数在不同收敛因子下的收敛曲线 |
Step1. 设置种群规模N=30, 维数dim=2, 最大迭代次数tmax=500, 搜索区间为[0, 1], 随机生成
Step2. 利用Chebyshev混沌映射策略初始化灰狼种群;
Step3. 将式(5)设置为适应度函数, 计算种群中所有灰狼个体的适应度值, 选择前三个最好的狼, 记录其位置Xα、Xβ和Xδ;
Step4. 利用公式(10)和(11)更新种群中其它灰狼个体的位置;
Step5. 利用公式(13)计算
Step6. 判断算法是否满足结束条件, 若达到预定的最大迭代次数tmax, 则停止计算, 输出最优位置
| 表 2 马斯京根模型出流量演算结果 |
4 应用实例
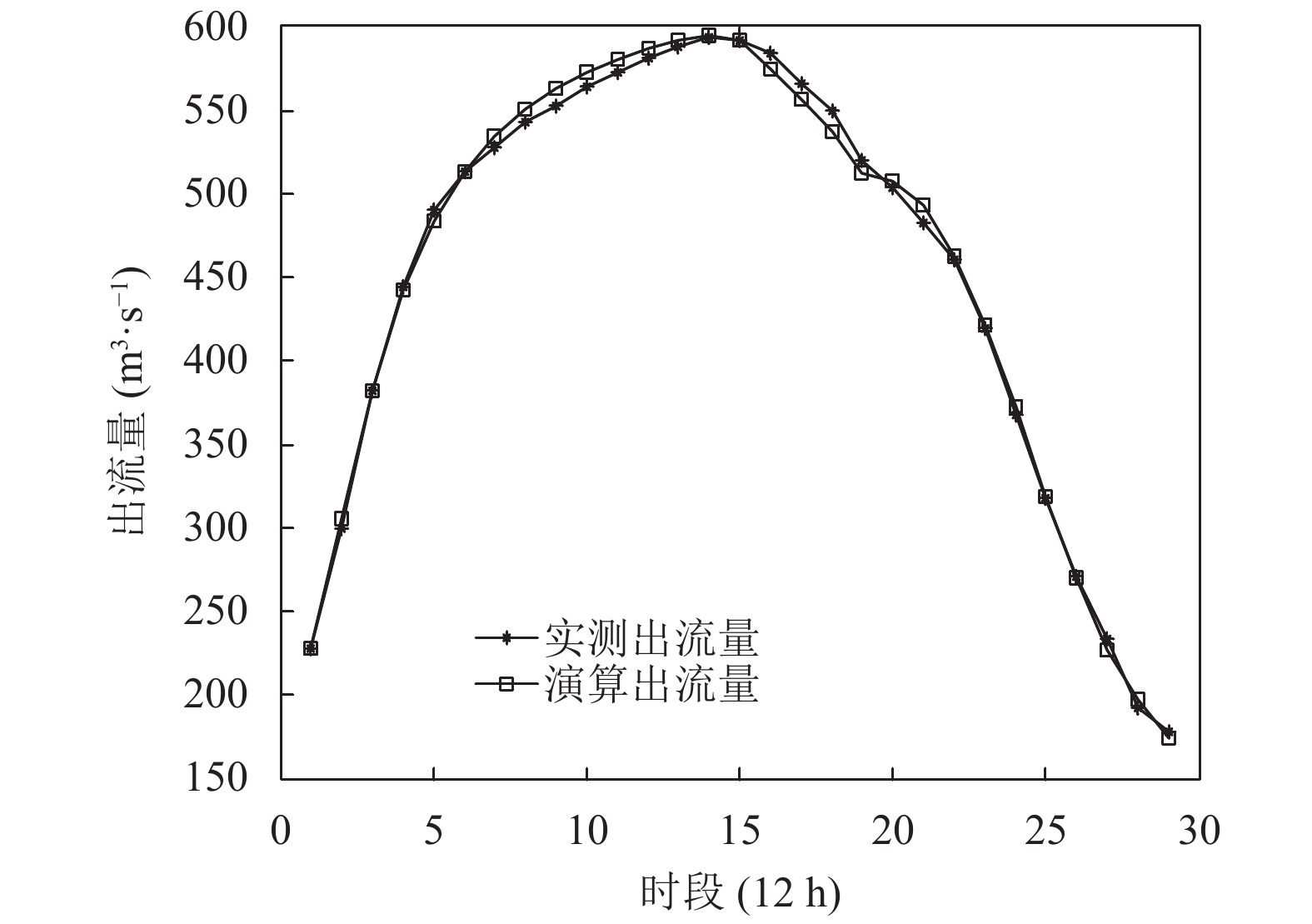
以南运河称沟湾至临清河段1961年8月的一次洪水过程的流量演算为例(该河段长83.8 km, 中间支流影响不明显), 数据来源于文献[9], 演算时段
|
图 8 IGWO算法洪水演算效果 |
|
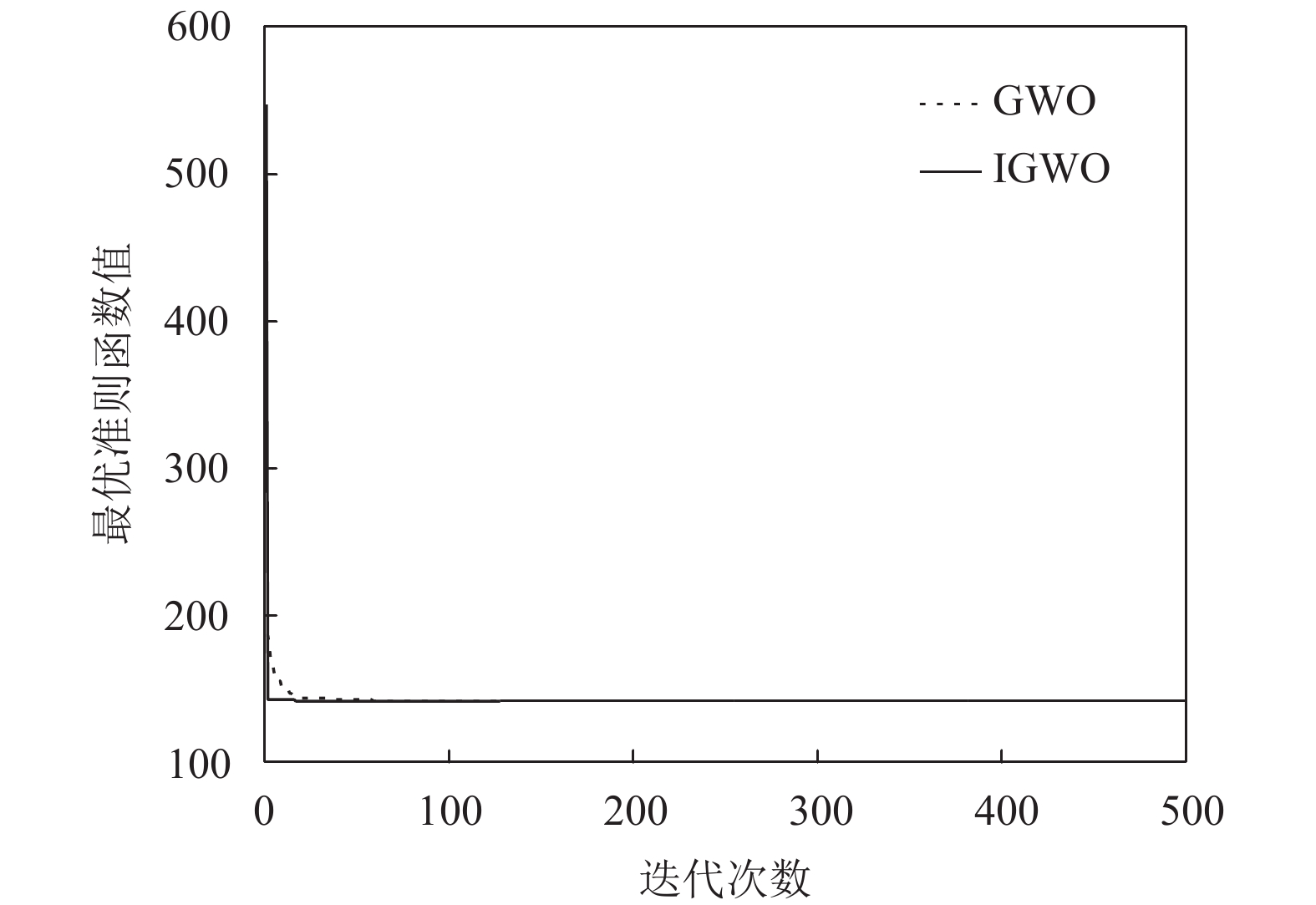
图 9 GWO和IGWO算法估计参数的迭代收敛曲线 |
从表2和表3的计算结果和各项评价指标评价的对比结果可以看出, 与现有的参数估计方法相比, IGWO算法所求得的最优化准则函数值, 平均绝对误差和平均相对误差更小, 表明利用该算法估计马斯京根模型参数具有更高的求解精度. 从图9可以看出, IGWO算法估计参数时收敛速度比基本GWO更快.
5 结论本文将改进的灰狼优化算法引入马斯京根模型, 对模型中的相关参数进行估计. 以南运河称沟湾至临清段1961年的洪水资料为例, 验证了IGWO算法求解马斯京根模型参数的有效性. 相比较于现有的其它参数估计方法, IGWO算法能很好地解决马斯京根模型的参数估计问题, 具有更高的求解精度和更好的实际应用价值.
| 表 3 各参数估计方法估计的参数和相关性能比较 |
| [1] |
Mccarthy GT. The unit hydrograph and flood routing. Proceedings of the Conference of North Atlantic Division. Rhode Island, USA. 1939.
|
| [2] |
詹道江, 徐向阳, 陈元芳. 工程水文学. 4版. 北京中国水利水电出版社, 2010.
|
| [3] |
Aldama AA. Least-squares parameter estimation for muskingum flood routing. Journal of Hydraulic Engineering, 1990, 116(4): 580-586. DOI:10.1061/(ASCE)0733-9429(1990)116:4(580) |
| [4] |
Yoon J, Padmanabhan G. Parameter estimation of linear and nonlinear muskingum models. Journal of Water Resources Planning and Management, 1993, 119(5): 600-610. DOI:10.1061/(ASCE)0733-9496(1993)119:5(600) |
| [5] |
黄兴春, 董增川, 陈甜, 等. 基于遗传算法的马斯京根模型参数优化. 水电能源科学, 2014, 32(7): 11-13, 22. |
| [6] |
王文川, 徐冬梅, 邱林. 差分进化算法在马斯京根模型参数优选中的应用. 水利科技与经济, 2009, 15(9): 756-758. DOI:10.3969/j.issn.1006-7175.2009.09.002 |
| [7] |
Ouyang AJ, Liu LB, Sheng Z, et al. A class of parameter estimation methods for nonlinear muskingum model using hybrid invasive weed optimization algorithm. Mathematical Problems in Engineering, 2015, 2015: 573894. |
| [8] |
崔东文, 金波. 飞蛾火焰优化算法在马斯京根模型参数优化中的应用. 人民珠江, 2016, 37(8): 30-34. DOI:10.3969/j.issn.1001-9235.2016.08.007 |
| [9] |
马玉新, 解建仓, 罗军刚. 基于免疫克隆选择算法的马斯京根模型参数估计. 计算机工程与应用, 2010, 46(34): 208-212. DOI:10.3778/j.issn.1002-8331.2010.34.063 |
| [10] |
Mirjalili S, Mirjalili SM, Lewis A. Grey wolf optimizer. Advances in Engineering Software, 2014, 69: 46-61. DOI:10.1016/j.advengsoft.2013.12.007 |
| [11] |
Gandomi AH, Yang XS. Chaotic bat algorithm. Journal of Computational Science, 2014, 5(2): 224-232. DOI:10.1016/j.jocs.2013.10.002 |
| [12] |
Zhu G P, Kwong S. Gbest-guided artificial bee colony algorithm for numerical function optimization. Applied Mathematics and Computation, 2010, 217(7): 3166-3173. DOI:10.1016/j.amc.2010.08.049 |
| [13] |
De Jong KA. An analysis of behavior of a class of genetic adaptive systems[Ph.D. thesis]. Ann Arbor, MI, USA: University of Michigan, 1975.
|
| [14] |
金菊良, 杨晓华, 丁晶. 标准遗传算法的改进方案——加速遗传算法. 系统工程理论与实践, 2001, 21(4): 8-13. DOI:10.3321/j.issn:1000-6788.2001.04.002 |
| [15] |
Wang WC, Kang YB, Qiu L. Optimal parameter estimation for muskingum model using a modified particle swarm algorithm. Proceedings of the 2010 Third International Joint Conference on Computational Science and Optimization. Washington, DC, USA. 2010. 153–156,
|
| [16] |
Yang XH, Yang ZF, Lu GH, et al. A gray-encoded, hybrid-accelerated, genetic algorithm for global optimizations in dynamical systems. Communications in Nonlinear Science and Numerical Simulation, 2005, 10(4): 355-363. DOI:10.1016/j.cnsns.2003.12.005 |
 2018, Vol. 27
2018, Vol. 27


