1 引言

压缩感知是数字化时代的一个重要手段, 它是针对被测信号的稀疏性而提出的, 近年来得到广泛的研究^[1].压缩感知主要有三个重要部分: 信号稀疏表示、测量矩阵的构建和重构算法. 其中重构算法是研究压缩感知问题的核心之一, 压缩感知问题在数学上讲就是解决优化问题. 针对这一问题学者们提出了一些优化算法. 例如Bregman迭代算法^[2]、原始对偶算法^[3,4]、正交匹配追踪算法OMP^[5]、截断牛顿内点法、基于交替方向算法、加速迭代收缩阈值算法、可分近似稀疏重建算法^[6–8]等. 但是这些方法都具有一定的局限与不足, 因此寻找高效、快速的重构算法具有重要的理论意义.

微分进化^[9]是比较新的基于群体的随机优化方法. 它具有简单、快速、鲁棒性好等特点, 它的基本思想是: 对种群中的每个个体 $i$ , 从当前种群中随机选择3个点, 以其中一个点为基础, 另外两个点为参照做一个扰动, 所得点与个体 $i$ 交叉后进行“自然选择”, 保留较优者, 实现这种种群的优化^[10].微分进化算法具有较好的全局优化性, 不容易陷入局部极值. 考虑到该算法的诸多优点, 本文对该算法进行改进, 提出了一种带约束的微分进化算法应用于压缩感知的求解中, 并进行了数值模拟.

2 问题描述

压缩传感的基本问题是对一个信号 $x \in {R^n}$ 进行传输, 为了节省空间资源需要对信号进行压缩处理, 即对其乘上一个“长而窄”矩阵, 亦即:

$Ax = b$

(1)

其中, $A \in {R^{m \times n}}(m \ll n)$ 称为压缩矩阵, $b \in {R^m}$ 为传输的信号.

在信号处理中一个重要的概念是稀疏性, 它是指信号中零分量在信号总长度中所占的比重, 若把信号 $x$ 中非零分量的个数记作0-范数 $({\left\| x \right\|_0})$ ,则信号重建问题可以变成等式约束优化问题:

$\left\{ \begin{gathered} \mathop {\min }\limits_{x \in {R^n}} {\left\| x \right\|_0}\; \hfill \\ Ax = b \hfill \\ \end{gathered} \right. $

(2)

上述问题是一个组合优化问题^[11], 不能使用已有的数学分析工具进行求解, 而且当维数增大时, 问题的复杂度也会增大, 为了更好的解决此类问题, 可以将上述优化问题转化为求解问题:

$\left\{ \begin{gathered} \mathop {\min }\limits_{x \in {R^n}} {\left\| x \right\|_p}\;\;\;\;\;\; \hfill \\ Ax = b \hfill \\ \end{gathered} \right.$

(3)

其中, $p > 0$ , ${\left\| x \right\|_p} = {(\sum\limits_{i = 1}^n {{{\left| {{x_i}} \right|}^p}} )^{1/p}}$ .

当 $p > 0$ 可以得出式(3)的稀疏解, 从下面的几何图形来说明. 考虑:

$\left\{ \begin{array}{l}\mathop {\min }\limits_{x \in {R^2}} {\left\| x \right\|_p} = \mathop {\min }\limits_{x \in {R^2}} ({\left| {{x_1}} \right|^p} + {\left| {{x_2}} \right|^p}){}^{\frac{1}{p}}\\a{x_1} + b{x_2} = c\end{array} \right.$

(4)

优化问题的目的是在图中所示直线上找到一点使得 ${l_p}$ 球的半径最小, 显然由于当 $0 < p < 1$ 时 ${l_p}$ 球是内凸的, 当半径逐渐增加时与直线的交点即优化问题的解将位于坐标轴上, 而这样的点是稀疏的, 当 $p = 1$ 时其中的菱形 ${l_1}$ 是特殊的, 在一定的条件下也会有稀疏解. 当 $p > 1$ 时 ${l_p}$ 球是外凸的, 当逐渐膨胀时与图像的切点一定不再坐标轴上, 即此时的解不是稀疏解. 而 ${l_2}$ 范数通常用来代表当 $p > 1$ 时的特例的.

求解式(3)实质上是一个优化问题, 本文主要对微分进化算法进行改进, 提出一种带约束的微分算法, 利用此方法求解式(3), 取得了较好的效果.

3 改进的微分算法

微分进化算法具有很好地全局优化性,是经典的全局优化算法, 该算法适用于无约束连续变量的全局优化问题, 包括线性规划、非线性规划、非光滑优化^[12].但是实际中我们会遇到一些带有约束条件的较复杂的问题, 所以我们采用改进的微分进化算法, 该算法在微分进化算法的基础上加入了对约束条件的处理.

设待求的优化问题如下:

$\left\{ \begin{gathered} \mathop {\min }\limits_{x \in {R^n}} F(x) \hfill \\ {g_k}(x) \leqslant 0\;\;(k = 1,2. \cdots ,m) \hfill \\ \end{gathered} \right.$

(5)

其中, $x \in S$ , $S$ 称为搜索空间. $F\left( {{x_i}} \right) = F\left( {X_1^i,X_2^i, \cdots ,X_n^i} \right)$ 为目标函数, ${g_k}( x ) \leqslant 0, ( k = $ $1,2, \cdots ,m )$ 为约束条件.

微分进化算法是经过编码和初始化、交叉、变异、选择等操作实现的, 而这些操作过程中参数的选择对微分进化算法的搜索性能有较大的影响, 微分进化算法的种群规模 $N$ 越大, 搜索能力会加强, 但也会增加微分进化的计算量, 一般取 $3n \sim 10n$ ( $n$ 为变量个数), 交叉概率因子 $Pc$ 是一个位于 $\left( {0,1} \right)$ 内的常数, 它决定了变异个体分量值代替前个体分量值的概率, 即它越大发生交叉的可能性越大. 变异因子F是用来控制差分向量的缩进, 它的取值范围一般在 $\left( {0,1} \right)$ .

改进微分进化算法选择的参数为种群的规模 $N$ 取 $10n$ ( $n$ 为变量个数), 交叉概率 $Pc$ 取0.1, 变异因子F取0.5, 在此基础上以上述约束优化问题(5)为例, 对标准微分进化算法进行改进, 主要表现在对约束条件进行处理的这一方面. 如下:

针对上述优化问题(5), $\Omega = X \in S;{g_k}(X) \leqslant 0, (k = 1,$ $2, \cdots ,m)$ 称为可行点集或可行区域, $S \subset {R^n}$ 称为搜索空间, 通常为 $n$ 维立方体, 即 ${l_i} \leqslant {x_i} \leqslant {u_i},(i = 1,2, \cdots ,n).\;f:$ $S \to R$ 称为目标函数, $n$ 是变量空间维数. 记:

${h_i}(X) = \left\{ \begin{array}{ll}0,&\text{if}\;{g_i}(X) \le 0\\{g_i}(X),& \text{else}\end{array} \right.$

(6)

$H(X) = \sum\limits_{i = 1}^m {{h_i}(X)} $

(7)

定义逻辑函数如下:

$better({X_1},{X_2}) = \left\{ \begin{array}{ll}\text{REAL},&\text{if}\;H({X_1}) < H({X_2})\\\text{FALSE},&\text{if}\;H({X_1}) > H({X_2})\\\text{REAL},&\text{if}\;(H({X_1}) = H({X_2})) \\ &\wedge (f({X_1}) \le f({X_2}))\\\text{REAL},&\text{if}\;(H({X_1}) = H({X_2})) \\ &\wedge (f({X_1}) > f({X_2}))\end{array} \right.$

(8)

对于个体 ${X_1}$ 和 ${X_2}$ , 如果 $better({X_1},{X_2})$ 为真则表示 ${X_1}$ 优于 ${X_2}$ , 否则 ${X_2}$ 优于 ${X_1}$ .

改进微分进化算法的步骤如下:

Setp 1. (初始化) 输入参数: 种群的规模 $N$ , 交叉概率 $Pc$ , 交叉因子F, 随机生成的初始种群 $P(0) = \{ {X_1}(0),$ ${X_2}(0), \cdots, {X_N}(0) \}$ 为个体的集合, 其中 ${X_i}(t) = (x_1^i(0),x_2^i(0), \cdots, $ $x_n^i(0)),i = 1,2, \cdots ,N$ .

Step 2. (个体评价) 将群体按逻辑函数 $better\left( {x,y} \right)$ 进行从好到坏排序, 排序后记为 $P\left( t \right) = \left( {{X_1},{X_2}, \cdots, {X_N}} \right)$ , 其中按顺序, ${X_1}$ 为最好的个体, ${X_N}$ 为最差的个体. 计算每个个体 ${X_i}(t)$ 的适应值 $F({X_i}(t))$ .

Step 3. (繁殖) 对种群中的每个个体 ${X_i}(t)$ , 随机生成4个互不相同的随机整数 ${r_1},{r_2},{r_3} \in \left\{ {1,2, \cdots ,N} \right\}$ 和 ${j_{rand}} \in \left\{ {1,2, \cdots ,n} \right\}$ .

$x_j^{i'}(t)=\left\{\begin{aligned}& x_j^{{r_1}}(t)+F\cdot (x_j^{{r_2}}(t)-x_j^{{r_3}}(t)), \\ & \quad\quad{\rm if}\;rand[0,1]< Pc\;{\rm{or}}\; j={j_{rand}}\\& {x_j^i(t),\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\rm else}}\end{aligned} \right.$

(9)

通过交叉变异产生的新个体:

$X_i'(t) = \left\{ {x{{_1^{(i)}}'}(t),x_2^{(i)'}(t), \cdots ,x_j^{(i)'}(t), \cdots ,x_n^{(i)'}(t)} \right\}$

(10)

Step 4. (选择) 当且仅当新个体的评价函数值更好时才被保留到下一代群体中, 否则, 父代个体仍然保留在群体中, 再一次作为下一代的父向量, 即得到:

$X(t + 1) = \left\{ \begin{array}{l}X_i'(t),\;\;\;\;\text{if}\;f(X_i'(t)) < f({X_i}(t))\\{X_i}(t),\;\;\;\;\;\;\;\;\;\;\;\;\text{else}\end{array} \right.$

(11)

Step 5. (终止检验) 如果种群 ${X_i}(t + 1)$ 满足终止条件, 则输出 ${X_i}(t + 1)$ 中具有最小适应值得个体为最优解, 否则转Step 2.

标准微分进化算法通过这种方式进行改进之后, 可以简单有效的处理等式约束和不等式约束. 具体的判断方法为: 用函数 $H(X)$ 来衡量违反约束的程度, $H(X)$ 的值大则视为坏个体, 当 $H(X)$ 的值相同时, 根据目标函数 $f(X)$ 来决定它们的优劣.

4 数值模拟

为了利用改进微分进化算法的求解, 将式(3)转化成求解上述问题:

$\left\{ \begin{array}{l}\mathop {\min }\limits_{x \in {R^n}} f(x) = \mathop {\min }\limits_{x \in {R^n}} {\left\| x \right\|_p}\\\left( {Ax - b} \right) \le 0\\ - \left( {Ax - b} \right) \le 0\end{array} \right.$

(12)

以下给出数值模拟:

$\text{模拟}1\quad\left\{ \begin{array}{l}\min \;{(\;{\left| {{x_1}} \right|^p} + {\left| {{x_2}} \right|^p})^{1/p}}\\2{x_1} + 3{x_2} = 5\end{array} \right.$

(13)

$\text{模拟}2\quad\left\{ \begin{array}{l}\min \;{(\;{\left| {{x_1}} \right|^p} + {\left| {{x_2}} \right|^p} + {\left| {{x_3}} \right|^p})^{1/p}}\\2{x_1} + 3{x_2} - {x_3} = 5\\{x_1} - {x_2} + {x_3} = 1\end{array} \right.$

(14)

$\text{模拟}3\quad\left\{ \begin{array}{l}\min \;\;{({\left| {{x_1}} \right|^p} + {\left| {{x_2}} \right|^p} + {\left| {{x_3}} \right|^p} + {\left| {{x_4}} \right|^p})^{1/p}}\\2{x_1} + 3{x_2} - {x_3} + {x_4} = 5\\{x_1} + 2{x_2} - 4{x_3} + {x_4} = 1\\2{x_1} - {x_2} + {x_3} + 3{x_4} = 6\end{array} \right.$

(15)

对上述未知数个数为2、3、4的约束优化问题利用改进微分进化算法进行求解, 主要控制参数选取为: 种群的规模 $N$ 取 $10n$ ( $n$ 为变量个数), 交叉概率 $Pc$ 取0.1, 交叉因子F取0.5, 最大演化代数取为5000代. 当 $p$ 取不同值时, 计算结果见表1至表3.

从表中可以看出当未知数个数为2、3且当 $0 < p < 1$ 时的稀疏解要比 $p = 1$ 时的好, 而当未知数个数为4或者更大时, $p = 1$ 时的稀疏解更好一些, 而不论变量个数是多少, $p = 2$ 时所求的解都不具有稀疏性. 为了进一步验证改进微分进化算法,下面给出改进微分进化算法与其它优化算法对比的模拟结果.

$\text{模拟}4\quad\left\{ \begin{array}{l}\min \;\;\left| {{x_1}} \right| + \left| {{x_2}} \right| + \left| {{x_3}} \right|\\2{x_1} + 3{x_2} - {x_3} = 5\\{x_1} - {x_2} + {x_3} = 1\end{array} \right.$

(16)

$\text{模拟}5\quad\left\{ \begin{array}{l}\min \;\;\left| {{x_1}} \right| + \left| {{x_2}} \right| + \left| {{x_3}} \right| + \left| {{x_4}} \right|\\2{x_1} + 3{x_2} - {x_3} + {x_4} = 5\\{x_1} + 2{x_2} - 4{x_3} + {x_4} = 1\\2{x_1} - {x_2} + {x_3} + 3{x_4} = 6\end{array} \right.$

(17)

下面将改进微分进化算法(RDE)与截断牛顿内点法(TNIPM)、可变分稀疏重建算法(SpaRSA)、基于交替方向算法的稀疏解(DAIM)、原始对偶内点算法(PDIPA)对比. 结果见表4和表5.

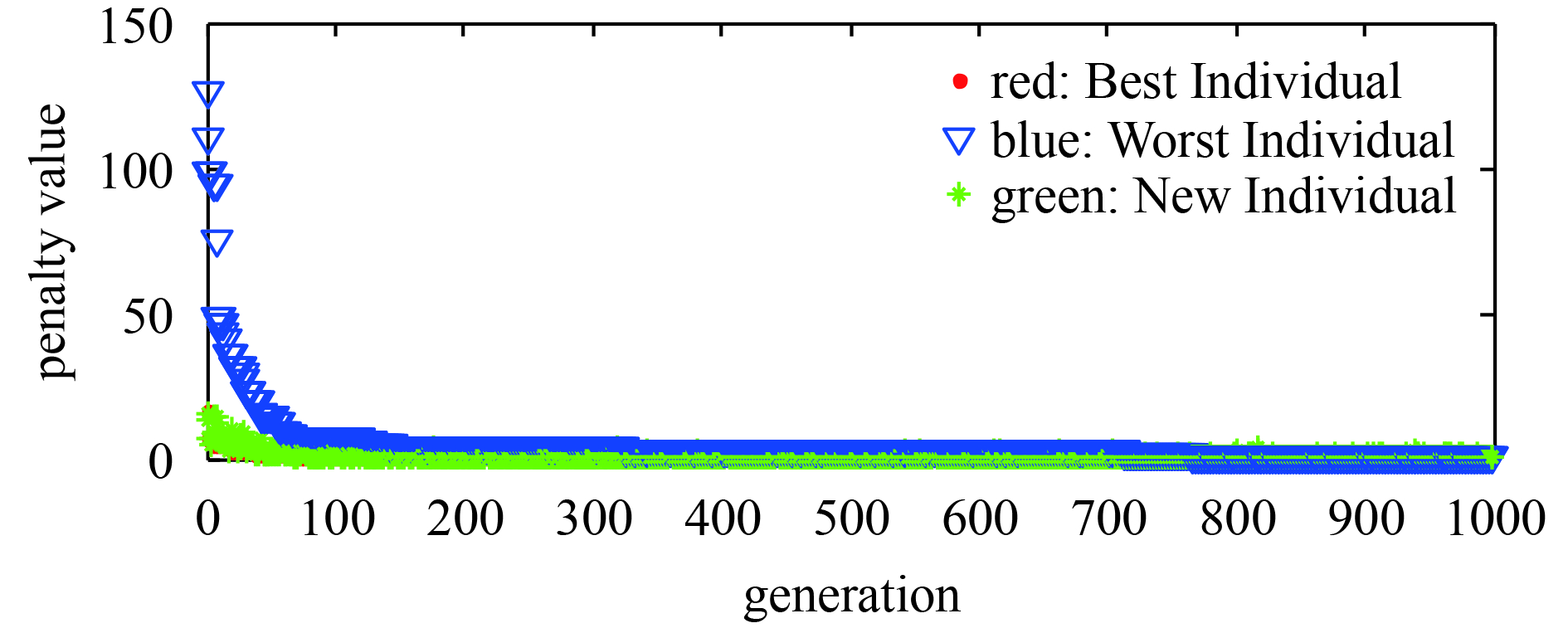
由表4、表5可以看出改进微分算法的稀疏解比其他优化算法的更好,在其它算法中原始对偶算法的稀疏解比截断牛顿内点法和基于交替方向算法的更好, 而可变分稀疏重建算法效果较差. 图2给出了迭代过程中最好、最差以及新个体的迭代图, 图中可以看出随着迭代次数的增加改进微分进化算法的适应值越来越好.

5 结论

本文在微分进化的基础上对其改进, 提出了一种寻优性、稳定性更好的改进微分进化算法, 将其应用到带约束的压缩感知求解中, 并给出了数值模拟, 模拟结果表明在改进微分算法中选择 ${l_p}(0 < p \leqslant 1)$ 范数得到的解具有较好的稀疏性, 而 ${l_2}$ 范数的求解方法得到的解并不具备稀疏性. 当维数较小时本文所提出的改进微分进化算法的稀疏解更准确.