2. 广东松山职业技术学院 计算机系, 韶关 512126
2. Department of Computer Science, Guangdong Songshan Polytechnic, Shaoguan 512126, China
聚类是在没有任何先验知识的指导下, 从样本集合中挖掘出潜在的相似模式, 并将其划分成多个组或簇的过程, 其目的是使得簇内相似度高, 而簇间相似度低, 数据对象的簇可以看做隐含的类, 聚类可以自动地发现这些类.由于在聚类过程中并没有提供类的标号信息, 因此, 聚类又被称做无监督学习, 对于无先验知识的样本来说, 如何对其聚类结果进行有效评价是国内外的研究热点, 许多经典的内部聚类评价指标先后被提出, 如CH, I, DB, SD, BWP等, 然而这些指标可能会受噪声等异常的影响, 因此, 如何改进或设计出更为科学合理的评价指标是聚类评价领域的一个重要研究方向.此外, 聚类结果评价除了和有效性指标本身有关, 还与所采用的聚类算法密不可分, 研究表明, 没有任何一种聚类算法可以得到所有数据集的最优划分[1], 而应用范围较广的K-means、K-medoids及其衍生算法[2]在实际应用中又存在一定的不足.为此, 本文对常用聚类评价指标进行了对比分析, 提出了一个新的评价指标, 并对K-medoids算法进行了改进, 在此基础上, 设计了聚类质量评价模型, 先后采用UCI数据集和KDD CUP99数据集对新模型进行了验证, 实验结果表明, 新评价指标的聚类数正确率明显高于其他四种常用指标, 聚类质量评价模型可以给出精准的聚类数范围.
1 研究现状 1.1 划分式聚类算法划分式聚类算法[3]在运算前需要人工预定义聚类数k, 再通过反复迭代更新各簇中心, 不断优化(降低)目标函数值, 逐渐逼近最优解, 完成最终聚类, K-means和K-medoids是两种典型的划分式聚类算法.K-means算法的簇中心是通过计算一个簇中对象的平均值来获取, 它根据数据对象与簇中心的距离完成"粗聚类", 再通过反复迭代, 将样本从当前簇划分至另一个更合适的簇来逐步提高聚类质量, 其核心思想是找出k个簇中心, 使得每个数据点到其最近的簇中心的平方距离和被最小化.该方法描述容易、实现简单快速, 是目前研究最多的聚类方法, 文献[4–6]从初始簇中心的选择、对象的划分、相似度的计算方法、簇中心的计算方法等方面对该经典算法进行了改进, 使其适用于不同的聚类任务, 但在使用中存在一些不足: 簇的个数难以确定; 聚类结果对初始值的选择较敏感; 算法容易陷入局部最优值; 对噪音和异常数据敏感; 不能用于发现非凸形状的簇, 或具有各种不同规模的簇.
当样本中存在一个或多个极值对象时, 采用均值算法会显著地扭曲数据的分布, 而平方误差函数的使用会进一步地扩大这一影响, 针对这一问题, K-medoids通过试图最小化所有对象与其所属簇的中心点之间的绝对误差之和的方式找出簇中心点.典型基于中心的划分方法有PAM、CLARA和CLARANS[7], 虽然K-medoids[8]算法对噪声和异常数据的敏感程度有所改善, 但仍依赖于初始类簇中心的随机选择, 且更新类簇中心时采用全局最优搜索, 故耗时较多. 文献[9]提出一种快速K-medoids算法, 从初始聚类中心选择、类簇中心更新方法两方面对PAM算法进行改进, 基本思想是: 首先计算数据集中每个样本的密度, 选择前k个位于样本分布密集区域的样本为初始聚类中心, 再将其余样本分配到距离最近的类簇中心, 产生初始聚类结果; 然后, 在每个类簇内部找一个新中心, 使该簇非中心样本到中心样本距离之和最小, 进而得到k个新中心; 最后按距离最近原则, 重新分配所有非中心样本到最近类簇中心, 如果本次迭代所得聚类结果与前一次不同, 则转至下一次迭代, 否则算法停止.在实际应用中, 该算法的初始中心在一定程度上存在过于集中的可能, 因此, 从样本的空间结构来看, 各中心点的分散程度不高, 代表性依然不足.
1.2 内部评价指标聚类有效性评价指标是对聚类结果进行优劣判断的依据, 通过比较指标值可以确定最佳聚类划分和最优聚类数, 在对聚类结果进行评估时, 内部评价指标在不涉及任何外部信息的条件下, 仅依赖数据集自身的特征和度量值, 通过计算簇内部平均相似度、簇间平均相似度或整体相似度来评价聚类效果的优劣和判断簇的最优个数.理想的聚类效果是簇内紧密且簇间分离, 因此, 常用内部评价指标的主要思想是通过簇内距离和簇间距离的某种形式的比值来度量的.
为便于对各指标和本文算法进行描述, 设样本集合X={x1, x2, …, xi, …, xN}, |X|=N, 各样本特征数为p, 该样本集由k个簇构成, 即X={C1, C2, …, Ck}, 每簇样本数为n, c为样本集的均值中心, 簇中心集合V={v1, v2, …, vk}(k<N), 常见的内部评价指标及其特点如下:
(1) DB指标(Davies-Bouldin Index)[10]
| $DB\left( k \right) = \dfrac{1}{k}\displaystyle\sum\limits_{{{i}} = {\rm{1}}}^{{k}} {{{ma}}{{{x}}_{{{j, j}} \ne {\rm{1}}}}} {\rm{ }}\dfrac{{\dfrac{1}{{{n_i}}}\displaystyle\sum\limits_{x \in {C_i}} {d\left( {x, {v_i}} \right) + \dfrac{1}{{{n_j}}}\displaystyle\sum\limits_{x \in {C_j}} {d\left( {x, {v_j}} \right)} } }}{{d\left( {{v_i}, {v_j}} \right)}}$ | (1) |
DB指标将相邻两簇的簇中各样本与簇中心的平均距离之和作为簇内距离, 将相邻两簇的簇中心间的距离作为簇间距离, 取二者比值最大者作为该簇的相似度, 再对所有簇的相似度取平均值得到样本集的DB指标.可以看出, 该指标越小意味着各簇间的相似度越低, 从而对应更佳的聚类结果. DB指标适合评价"簇内紧凑, 簇间远离"的数据集, 但当数据集的重叠度较大(如:当遇到环状分布数据时), 由于各簇的中心点重叠, 因此DB指标很难对其形成正确的聚类评价.
(2) CH指标(Calinski-Harabasz)[11]
| $CH\left(k \right)={ }\dfrac{{\displaystyle\sum\limits_{\rm{i}=\rm{1}}^{\rm{k}}{{{n}_{i}}{{d}^{2}}\left({{v}_{i}}, c \right)}}/{\left(k-1 \right)}\; }{\displaystyle\sum\limits_{i=1}^{\rm{k}}{{\displaystyle\sum\limits_{\rm{x}\in {{\rm{C}}_{\rm{i}}}}^{{}}{{{d}^{2}}\left(x, {{v}_{i}} \right)}}/{\left(N-k \right)}\; }}$ | (2) |
CH指标将各簇中心点与样本集的均值中心的距离平方和作为数据集的分离度, 将簇中各点与簇中心的距离平方和作为簇内的紧密度, 将分离度与紧密度的比值视为CH的最终指标.该指标越大表示各簇之间分散程度越高, 簇内越紧密, 聚类结果越优. Milligan在文献[12]中, 对CH等评价指标的性能进行了深入探讨, 实验结果表明:CH指标在多数情况下, 都要优于其它的指标, 但当聚类数趋近于样本容量N时, 各样本自成一簇, 簇中心即为样本自身, 此时簇内距离和约等于0, 分母为极小值, CH指标将趋于最大, 此时的聚类评价结果无实际意义.
(3) XB指标(Xie-Beni)[13]
| $XB\left( k \right) = {\rm{ }}\dfrac{{\displaystyle\sum\limits_{i = 1}^k {\displaystyle\sum\limits_{x \in {{\rm{C}}_{\rm{i}}}} {{d^2}\left( {x, {v_i}} \right)} } }}{{{\rm{n}} \times {{\min }_{i, j \ne i}}{d^2}\left( {{v_i}, {v_j}} \right)}}$ | (3) |
和CH指标一样, XB也是将簇内紧密度与簇间分离度的比值作为指标的表达式, 期望在簇内紧密度与簇间分离度之间寻找一个新的平衡点, 使其达到一个理想化的极值, 从而得到最优的聚类结果. 与CH指标不同是: XB指标使用最小簇中心距离的平方作为整个样本集的分离度.
(4) Sil指标(Silhouette-Coefficient)[14]
| $Sil\left( k \right) = {\rm{ }}\frac{{\rm{1}}}{{\rm{k}}}\sum\limits_{i = 1}^k {\left\{ {\frac{1}{{{n_i}}}\sum\limits_{x \in {C_i}} {\frac{{b\left( x \right) - a\left( x \right)}}{{\max \left[ {b\left( x \right), a\left( x \right)} \right]}}} } \right\}} $ | (4) |
式中, a(x)是样本x所属簇的簇内凝聚程度, 用x与其同一个簇内的所有元素距离的平均值来表示, 凝聚度a(x)定义为:
| $a\left( x \right) = \frac{1}{{{n_i} - 1}}\sum\limits_{x, y \in {C_i}, y \ne x} {d\left( {x, y} \right)} $ | (5) |
式中, b(x)是样本x与其他簇的簇间分离程度, 用x与其它簇之间平均距离的最小值来表示, 分离度b(x)定义为:
| $b\left( x \right) = {\min _{j, j \ne i}}\left[ {\frac{1}{{{n_j}}}\sum\limits_{x \in {c_i}, y \in {c_j}} {d\left( {x, y} \right)} } \right]$ | (6) |
从式(4)可以看出, 当簇内距离减小, 簇间距离增大时, Sil指标值增大, 聚类结果趋于理想, 因此, 要取得最佳聚类, 就需要减少簇内各点之间的距离, 同时增大簇间的距离.然而, 与CH指标类似, 当数据接近散点状分布时, 聚类结果并不理想, 此外, 当数据成条状分布的时, 各簇中心非常接近, 且聚类结果非常理想, 但Sil指标此时最小, 并不能对聚类结果做出客观的评价.
2 聚类质量评价模型聚类质量评价模型由聚类算法和内部评价指标两部分构成, 鉴于K-medoids算法及其改进算法在初始聚类中心选择阶段存在的问题, 以及上述常用内部评价指标存在的缺陷, 本文对二者分别进行了改进, 具体如下.
2.1 改进K中心点聚类算法本文在文献[7,8]的基础上, 选取被其他样本紧密围绕且相对分散的数据对象作为初始聚类中心, 使得中心点在确保自身密度较大的同时还具备良好的独立性.基本思路是: 首先通过计算样本集中各样本间的距离得到样本集的距离矩阵; 将样本集与各样本的平均距离的比值作为样本的密度, 选取密度值最高的α个样本存入高密度点集合H中, α表示候选代表点在样本集中所占的比例, 该值可由用户指定, 本文实验环节中的α值为30%; 从集合H中选取相对分散且具有较高密度的初始中心存入集合V, 即V={v1, v2, …, vk}. 最后, 借鉴文献[7]的算法, 将各样本按最小距离分配至相应簇中, 重复这一过程, 直至准则函数收敛, 本文算法的定义和公式如下.
定义1. 空间任意两点间的欧氏距离定义为
| $d\left( {{x_i}, {x_j}} \right) = \sqrt {\sum\limits_{w = 1}^p {{{\left( {x_i^w - x_j^w} \right)}^2}} } {\rm{ }}$ | (7) |
其中, i=1, 2, …, N; j=1, 2, …, N
定义2. 数据对象xi的平均距离定义为:xi与全部样本的距离之和除以样本集的总个数.
| $Dist\left( {{x}_{i}} \right)={\sum\limits_{j=1}^{N}{d\left( {{x}_{i}}, {{x}_{j}} \right)}}/{N}\; $ | (8) |
定义3. 样本集的平均距离定义为:各数据对象间的距离总和除以从样本集中任选两个对象的所有排列次数.
| $DistMean=\sum\limits_{i=1}^{N}{{\sum\limits_{j=1}^{N}{d\left( {{x}_{i}}, {{x}_{j}} \right)}}/{A_{N}^{2}}}$ | (9) |
定义4. 数据对象xi的密度定义为:样本集的平均距离与数据对象xi的平均距离的比值.
| $Density\left( {{x}_{i}} \right)={DistMean}/{Dist\left( {{x}_{i}} \right)}$ | (10) |
定义5. 数据对象xi与所属簇的各数据对象的距离之和为:
| $Dist{S\!um}\left( {{x_i}} \right) = \sum\limits_{j = 1}^{{n_i}} {d\left( {{x_i}, {x_j}} \right)} {\rm{ }}$ | (11) |
其中, xi, xj∈Ct, t=1, 2, …, k
定义6. 簇Ct的簇内距离和矩阵为:
| $DistS\!um\left( {{C_t}} \right) = \left[ {\begin{array}{*{20}{c}} {DistS\!um\left( {{x_1}} \right)} \\ {DistS\!um\left( {{x_2}} \right)} \\ {\cdots} \\ {DistS\!um\left( {{x_n}} \right)} \end{array}} \right]$ | (12) |
其中, t=1, 2, …, k
定义7. 数据对象xi在簇更新过程中被视为簇中心的条件为:
| $DistS\!um({x_i}) = \min \left( {DistS\!um({C_t})} \right)$ | (13) |
其中, xi∈Ct, t=1, 2, …, k
定义8. 聚类误差平方和E的定义为
| $E = \sum\limits_{t = 1}^k {{{\sum\limits_{j = 1}^{{n_t}} {\left| {{x_{tj}} - {v_t}} \right|} }^2}} $ | (14) |
其中, xtj是第t簇的第j个数据对象, vt是第t簇的中心.
2.2 聚类有效性指标Improve-XB在对无先验知识样本的聚类结果进行评价时, 通常将“簇内紧密, 簇间分离”作为内部评价的重要标准, 文献[11]和文献[13]将各簇中心之间的距离作为簇间距离, 可能会出现因簇中心重叠而导致聚类评价结果失效等问题, 为此本文提出: 使用两个簇的最近边界点间的距离取代簇中心之间的距离, 为了便于分析, 以图1所示的人工数据集进行说明, 该数据集由三个环形结构的簇构成, 各簇中心极为接近, 从DB、XB指标公式可知, 在计算该数据集的簇间距离时, 由于簇中心点趋于重叠, 必然会出现簇间距离近似于0的情况, 当以"簇内紧密, 簇间分离"作为评判依据时, 意味着此时簇间的相似度极高, 从聚类划分的角度来看, 应将二者合并为一簇以提高聚类质量, 而事实上, 这种错误的划分将导致图1的最终聚类全部合并为一个簇, 这显然与真实的结果有着明显偏差.而本文使用簇间最近边界点间的距离表示簇间距离, 则可以从几何特征上确保各簇的结构差异性, 进而避免簇间距离为0现象的发生, 最大程度地反映出簇间的相似程度, 克服了环状中心点因重叠而导致的聚类结果合并等问题, 新指标IXB定义及公式如下.
定义9. 簇内紧密度(Compactness)定义为:各样本与所属簇的中心点的距离平方和. 实质为:
| $Comp\left( k \right) = \sum\limits_{i = 1}^k {\sum\limits_{x \in {C_i}} {{d^2}\left( {x, {c_i}} \right)} } $ | (15) |
定义10. 簇间分离度(Separation)定义为:簇间最邻近边界点的距离平方和与簇内样本个数的乘积.
| $S\!e\!p\left( k \right) = n \cdot {\min _{i, j \ne i}}{d^2}\left( {{x_i}, {x_j}} \right)$ | (16) |
其中, xi和xj是簇Ci
定义11. IXB指标定义为簇内紧密度与簇间分离度的比值与其倒数之和, 即实质为:
| $IXB\left( k \right) = \frac{{S\!e\!p}}{{Comp}} + \frac{{Comp}}{{S\!e\!p}}$ | (17) |
定义12. 最优聚类数k定义为IXB(k)取最大值时的聚类数目, 即:
| ${k_{opt}} = \mathop {\arg \max }\limits_{{k_{\min }} \leqslant k \leqslant {k_{\max }}} \left\{ {IXB\left( k \right)} \right\}$ | (18) |
其中, kmin=2, kmax采用文献[15]的AP算法得到.

|
图 1 环状分布数据集 |
IXB指标由两部分组成: Sep/Comp随着聚类数k的增加而递增, Comp/Sep随着聚类数k的增加而递减, 可以看出, IXB指标通过制衡Sep/Comp和Comp/Sep之间的关系, 确保了最优聚类划分, IXB越大, 意味着聚类质量越好.
2.3 聚类质量评价模型描述将改进的K中心点算法与IXB指标相结合, 构建聚类质量评价模型如图2所示, 模型描述如下:

|
图 2 聚类质量评价模型 |
(1) 根据式(6)~(8)依次计算整个样本集的任意两点间的欧氏距离、各数据对象的平均距离和样本集的平均距离.
(2) 根据式(10)计算各数据对象的密度, 选取密度值最高的α个样本存入候选初始中心集合H中, 令k=2.
(3) 根据式(6)将集合H中相距最远的两个高密度点v1和v2存入初始中心集合V中.
(4) 从H中选择满足与v1、v2距离乘积最大的v3,将其存储至V中.依次类推, 得到相对分散且具有较高密度的初始中心集合V,V={v1, v2, …, vk}.
(5) 在更新簇中心阶段, 根据式(11)、式(12)得到簇内距离和矩阵, 根据式(13)选出新的簇中心, 沿用文献[7]的算法, 将各样本按最小距离分配至相应簇中, 重复这一过程, 直至准则函数式(14)收敛.
(6) 使用式(17)计算IXB指标, 对当前聚类结果进行评价, 令k=k+1, 重复步骤(4), 直至k=kmax.
(7) 使用式(18), 将IXB取最大值时的k值作为最优聚类数.
2.4 模型的性能分析本文算法将样本集与各样本的平均距离比值作为样本的密度, 将高密度点视为候选簇中心, 确保了聚类中心的代表性, 使用最大乘积法对高密度点进行二次筛选, 增强了候选簇中心在空间上的离散程度, 使得聚类中心兼具代表性和分散性, 提高了逼近全局最优解的概率, 这样选择的初始聚类中心更符合样本的分布特征, 甚至有可能位于真实的簇中心, 因此, 所得到的初步聚类划分与样本的真实分布更加接近.在聚类结果评价方面, 通过将簇间最邻近边界点的距离平方和与簇内样本个数的乘积作为簇间分离度, 在簇内紧密度与簇间分离度之间寻找一个新的平衡点, 从而得到一个理想化的极值, 通过搜索该极值, 即可有效地完成最优聚类划分, 确定最优聚类数目k, 从而得到更好的聚类结果, 从整体上提升无先验知识样本的检测率和分类正确率等评价指标.
3 实验结果与分析实验分为两个部分, 第一部分对聚类质量评价模型的有效性进行了验证: 首先选用表1中的UCI数据集对本文算法和其他改进算法的准确率、迭代次数、总耗时进行了对比测试, 然后使用本文算法依次结合IXB及其它4个评价指标完成了聚类数对比测试; 第二部分将模型应用于数据集KDD CUP99, 从检测率、分类正确率、漏报率三个方面验证模型的实用性.本文实验环境: Intel(R) Core(TM) i3-3240 CPU @3.40 GHz, 8 GB内存, Win10专业版, 实验平台Matlab 2011b.
| 表 1 实验数据 |
3.1 聚类质量评价模型的有效性测试
(1) 改进聚类算法的对比测试
从表2~表4的实验对比结果可以看出, 改进聚类算法的聚类准确率、迭代次数和总耗时全部优于其他四种算法, 主要原因在于K中心点的初始中心随机分布令迭代次数与总耗时同时增加, 而文献[7]的初始中心点过于集中, 文献[8]的初始中心虽然具有一定的分散性, 但每次迭代都将簇平均值作为簇中心, 个别维度存在受异常数据影响的隐患, 因此, 本文算法的整体耗时要低于文献[7,8]算法.需要特别指出的是, 由于本文算法的初始聚类中心同时兼具代表性和分散性, 不仅提高了聚类准确率, 同时还降低了算法后期的迭代次数, 因此, 对算法的运算效率的提升产生了正向的推动作用.
| 表 2 聚类准确率比较 |
| 表 3 迭代次数 |
| 表 4 聚类总耗时(单位: s) |
(2) IXB指标的有效性对比测试
观察表5可知, IXB在5个UCI数据集上的聚类数正确率为80%, 而DB、CH、XB和Sil指标依次为40%, 60%, 40%, 60%, IXB指标的聚类数正确率明显高于其他四种指标.
3.2 聚类质量评价模型在KDD CUP99中的应用本实验环节选取KDD CUP99[16]训练集中的17330条记录作为训练数据, 从corrected数据集中随机抽取11420条数据作为测试集用于检验模型的性能.为提高整体运行效率, 在数据预处理方面, 首先使用独热编码完成字符数据的格式转换, 再通过属性简约法将数据集的41个特征约简为15个[17], 最后将数据集归一化处理, 形成新样本集, KDD CUP99数据描述如表6.
| 表 5 各内部评价指标聚类数对比 |
| 表 6 KDD CUP99数据集 |
(1) 最优k值的获取
借鉴文献[15], 使用AP算法对样本集完成"粗聚类"得到训练集的最大聚类数kmax=29, 如图3所示, 在训练过程中, 当15≤k≤20时, K中心点算法的IXB增幅较大, 当k=20时, IXB达到峰值, 此后, 随着k值的不断增大, IXB总体呈下降趋势; 文献[8], 文献[9]和本文算法的IXB随着k值的不断增大而缓慢增加, 当25≤k≤28时, 三种算法的IXB依次达到峰值, 此后随着k值的再次增大, IXB缓慢下降. 由定义11可知, 当IXB最大时k值即为最优, 因此, 三种算法使用IXB得到训练集的最优k值分别为: k文献[8]=26, k文献[9]=28, k本文算法=28.
(2) IXB对入侵检测指标的影响
在验证IXB是否有助于提高检测精度的环节中, 将图3中IXB缓慢上升至峰值, 再从峰值缓慢下降的这一阶段所对应的多个连续k值定义为最优聚类数范围, 并对该范围内的各入侵检测指标进行对比, 由于K中心点算法的随机性较强, 各项指标与k值之间无明显规律可循, 因此, 这里仅对其他三种算法的结果进行统计与分析.

|
图 3 训练集的IXB-K的关系图 |
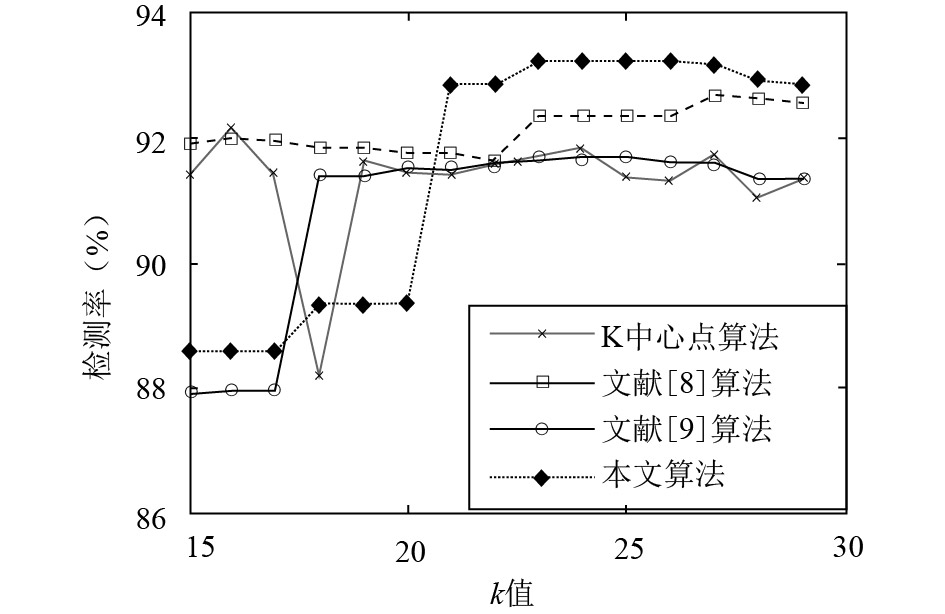
如图4所示, 当聚类数在[26, 28]范围内时, 3种算法的检测率达到了最大, 分别是: 92.68%、91.69%、93.2%.
|
图 4 不同k值的检测率 |
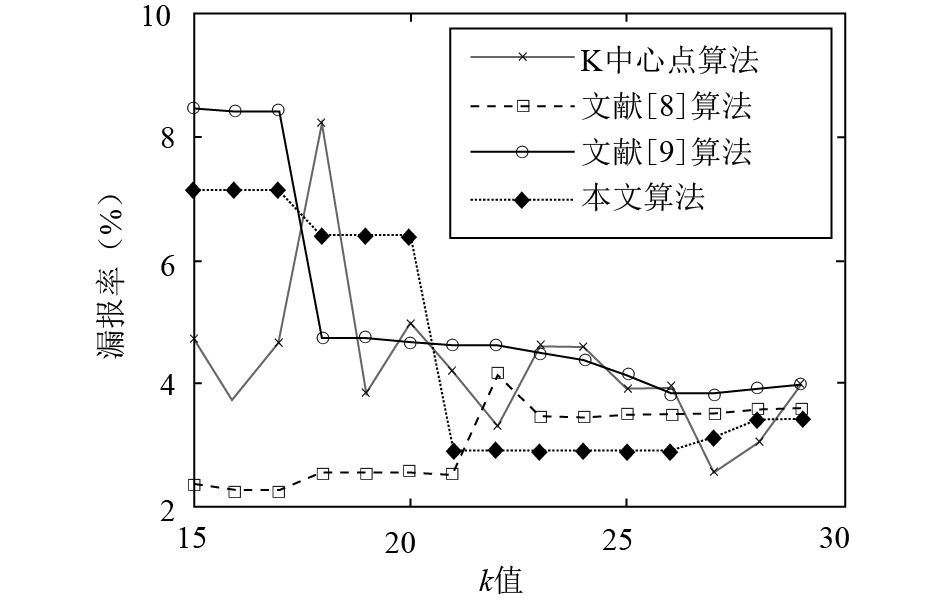
从图5的漏报率对比结果中可以看出: 当聚类数在[26, 27]范围内时, 文献[8]和本文算法的漏报率最小, 分别是: 3.81%、2.86%.
|
图 5 不同k值的漏报率 |
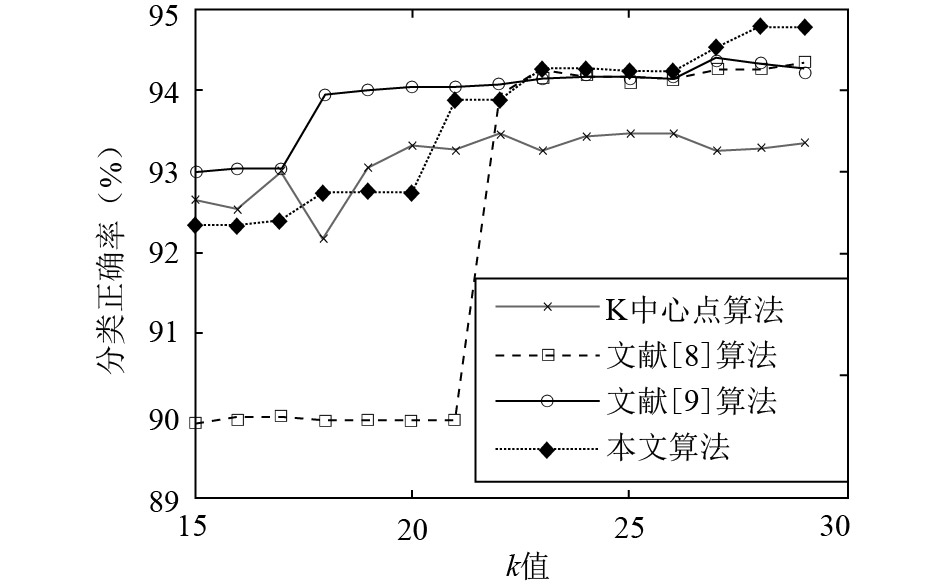
图6的正确分类率结果表明: 当聚类数在[27, 28]范围内时, 3种算法的正确分类率达到最大, 分别是: 94.27%、94.38%、94.78%. 从图4~6可以看出, IXB越大, 入侵检测指标越优. 综上所述, 本文提出的IXB能够合理、客观地评价聚类结果, 能够准确地反映出聚类质量, 可以为无先验知识样本集的有效聚类提供重要参考依据.
|
图 6 不同k值的分类正确率 |
5 结语
针对K中心点算法的初始聚类中心代表性不足, 稳定性差等问题, 提出了一种改进的K中心点算法, 将样本集与样本的各自平均距离比值作为样本的密度参数, 采用最大距离乘积法选择密度较大且距离较远的k个样本作为初始聚类中心, 兼顾聚类中心的代表性和分散性.针对常用内部评价指标在聚类评价中的局限性, 提出将簇间边界最近点的距离平方作为整个样本集的分离度, 定义了以簇内紧密度与簇间分离度的比值与其倒数之和为度量值的内部评价指标IXB, 结合改进的K中心点算法设计了聚类质量评价模型.在UCI数据集的测试表明, IXB指标的聚类数正确率明显高于其他四种常用指标, 在KDD CUP99数据集的实验结果表明, 本文提出的聚类质量评价模型可以给出精准的聚类数范围, 能够在保持较低漏报率的同时, 有效提高入侵检测率和分类正确率.
| [1] |
唐益明, 丰刚永, 任福继, 等. 面向结构复杂数据集的模糊聚类有效性指标. 电子测量与仪器学报, 2018, 32(4): 119-127. DOI:10.13382/j.jemi.2018.04.017 |
| [2] |
邹臣嵩, 杨宇. 基于最大距离积与最小距离和协同K聚类算法. 计算机应用与软件, 2018, 35(5): 297-301, 327. DOI:10.3969/j.issn.1000-386x.2018.05.053 |
| [3] |
邵东恒, 杨文元, 赵红. 应用k-means算法实现标记分布学习. 智能系统学报, 2017, 12(3): 325-332. DOI:10.11992/tis.201704024 |
| [4] |
刘美玲, 黄名选, 汤卫东. 基于离散量优化初始聚类中心的k-means算法. 计算机工程与科学, 2017, 39(6): 1164-1170. DOI:10.3969/j.issn.1007-130X.2017.06.021 |
| [5] |
徐鹏程, 王诚. K-Means算法改进及基于Spark计算模型的实现. 南京邮电大学学报(自然科学版), 2017, 37(4): 113-118. DOI:10.14132/j.cnki.1673-5439.2017.04.018 |
| [6] |
王国辉, 林果园. 基于图聚类的入侵检测算法. 计算机应用, 2011, 31(7): 1898-1900. DOI:10.3724/SP.J.1087.2011.01898 |
| [7] |
谢娟英, 周颖. 一种新聚类评价指标. 陕西师范大学学报(自然科学版), 2015, 43(6): 1-8. DOI:10.15983/j.cnki.jsnu.2015.06.161 |
| [8] |
Van Der LaanM, Pollard K, Bryan J. A new partitioning around medoids algorithm. Journal of Statistical Computation and Simulation, 2003, 73(8): 575-584. DOI:10.1080/0094965031000136012 |
| [9] |
Park HS, Jun CH. A simple and fast algorithm for K-medoids clustering. Expert Systems with Applications, 2009, 36(2): 3336-3341. DOI:10.1016/j.eswa.2008.01.039 |
| [10] |
Davies DL, Bouldin DW. A cluster separation measure. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1979, 2(2): 224-227. DOI:10.1109/TPAMI.1979.4766909 |
| [11] |
Caliński T, Harabasz J. A dendrite method for cluster analysis. Communications in Statistics, 1974, 3(1): 1-27. DOI:10.1080/03610927408827101 |
| [12] |
Milligan GW, Cooper MC. An examination of procedures for determining the number of clusters in a data set. Psychometrika, 1985, 50(2): 159-179. DOI:10.1007/BF02294245 |
| [13] |
Xie XL, Beni G. A validity measure for fuzzy clustering. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1991, 13(8): 841-847. DOI:10.1109/34.85677 |
| [14] |
Rousseeuw P J. Silhouettes: a graphical aid to the interpretation and validation of cluster analysis. Journal of Computational and Applied Mathematics, 1987, 20: 53-65. DOI:10.1016/0377-0427(87)90125-7 |
| [15] |
王开军, 张军英, 李丹, 等. 自适应仿射传播聚类. 自动化学报, 2007, 33(12): 1242-1246. DOI:10.16383/j.aas.2007.12.017 |
| [16] |
Bolón-Canedo V, Sánchez-Maroño N, Alonso-Betanzos A. Feature selection and classification in multiple class datasets: An application to KDD Cup 99 dataset. Expert Systems with Applications, 2011, 38(5): 5947-5957. DOI:10.1016/j.eswa.2010.11.028 |
| [17] |
吴建胜, 张文鹏, 马垣. KDDCUP99数据集的数据分析研究. 计算机应用与软件, 2014, 31(11): 321-325. DOI:10.3969/j.issn.1000-386x.2014.11.081 |
 2019, Vol. 28
2019, Vol. 28


